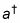¿Cómo encontrar el estado propio de energía de un oscilador armónico en el espacio posición
En la física cuántica, puede utilizar los operadores para determinar el estado propio de energía de un oscilador armónico en el espacio posición. El encanto de la utilización de los operadores la y
es que, dado el estado de la tierra, | 0>, los operadores permiten encontrar todos los estados de energía sucesivos. Si usted quiere encontrar un estado excitado de un oscilador armónico, se puede comenzar con el estado fundamental, | 0>, y aplicar el operador de fondos,
Por ejemplo, usted puede hacer esto:
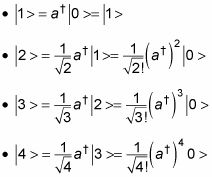
Etcétera. En general, usted tiene esta relación:
¿No puedes conseguir un estado propio espacial de este vector propio? Algo como
no sólo | 0>? Sí puedes. En otras palabras, usted quiere encontrar
Por lo que necesita las representaciones de
en el espacio posición.
los p operador se define como
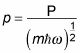
Porque
puedes escribir
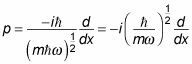
Y la escritura
esto se convierte
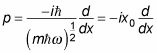
Bien, ¿qué pasa con la la operador? Tu sabes
Y eso
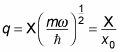
Por Consiguiente,
También puede escribir esta ecuación como
Bueno, por lo que es la en la representación posición. Cuál es
Eso resulta ser la siguiente:
Ahora es el momento de ser inteligente. Usted desea resolver | 0> en el espacio de la posición, o lt; X | 0>. Aquí está la parte más inteligente - cuando se utiliza el operador de la reducción, la, on | 0>, usted tiene que conseguir 0 porque no hay estado más bajo que el estado fundamental, por lo que la | 0> = 0. Y la aplicación de la lt; X | sujetador le da lt; X | la | 0> = 0.
Eso es inteligente porque va a darle una ecuación diferencial homogénea (es decir, uno que es igual a cero). En primer lugar, usted sustituye por la:
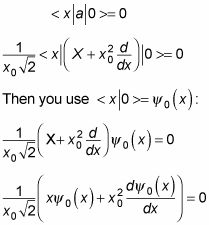
Multiplicando ambos lados por
le da la siguiente
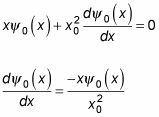
La solución a esta ecuación diferencial es compacto
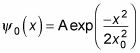
Eso es una función gaussiana, por lo que el estado fundamental de un oscilador armónico cuántico es una curva de Gauss, como se ve en la figura.
-
Aplicando la ecuación schr & # 246-dinger en tres dimensiones -
La determinación de la parte radial de una función de onda -
Encuentra los valores propios de la subida y bajada operadores del momento angular -
Cómo operadores de spin se asemejan a los operadores del momento angular -
Cómo crear estados propios del momento angular -
Cómo obtener la ecuación 246-dinger schr & #
Cómo determinar estados propios osciladores armónicos de un sistema En la física cuántica, cuando tienes los estados propios de un sistema, se puede determinar los estados permitidos de sistema y la probabilidad relativa de que el sistema estará en cualquiera de esos estados.El conmutador de los operadores A, B…
Cómo determinar las energías permitidas de un átomo de hidrógeno Cuando se aplica el Schr # 246-dinger ecuación mecánica cuántica para un átomo de hidrógeno, la condición de cuantificación para la función de onda r para permanecer como finito r# 32 va al infinito esdóndeSustituyendoen la ecuación de…
¿Cómo encontrar cualquier estado excitado de un oscilador armónico Si puede determinar la función de onda para el estado fundamental de un oscilador armónico cuántico, entonces usted puede encontrar cualquier estado excitado de ese oscilador armónico.Por lo tanto, si usted sabe lo queparece, se puede determinar…
¿Cómo encontrar los niveles de energía cuadrados así En la física cuántica, no sé si las condiciones de contorno de un cuadrado bien, usted puede encontrar theenergy niveles de un electrón.La ecuacionle dice que usted tiene que utilizar las condiciones de contorno para encontrar las constantes A y…
¿Cómo encontrar el nivel de energía de un oscilador armónico: un ejemplo Su instructor física cuántica puede pedirle que encontrar el nivel de energía de un oscilador armónico. La mejor manera de aprender es a través de un ejemplo. Digamos que usted tiene un protón someterse oscilación armónica concomo se muestra…
¿Cómo encontrar la energía de un oscilador cargada utilizando la teoría de la perturbación En la física cuántica, cuando se tiene los valores propios exactas para un oscilador cargada en un sistema perturbado, puede encontrar la energía del sistema. Basado en la teoría de la perturbación, la energía corregida del oscilador está…
¿Cómo encontrar la función de onda del estado fundamental de un oscilador cuántico En la física cuántica, se encuentra la función de onda del estado fundamental de un oscilador cuántico, como la que se muestra en la figura, que toma la forma de una curva de Gauss.El estado fundamental de un oscilador armónico mecánica…
Cómo utilizar los operadores de creación y aniquilación de resolver problemas oscilador armónico Creación y aniquilación pueden sonar como grandes tipos make-or-break-del-universo de ideas, pero jugar un papel protagonista en el mundo cuántico cuando se trabaja con osciladores armónicos. Utiliza los operadores de creación y aniquilación…
Cómo utilizar operadores lineales en la física cuántica En la física cuántica, lo que necesita saber cómo usar los operadores lineales. Un operador A se dice que es lineal si cumple con las siguientes condiciones:Por ejemplo, la expresiónen realidad es un operador lineal. Para entender esto, usted…
Cómo utilizar los operadores para las cantidades de la física cuántica En la física cuántica, puede utilizar los operadores para ampliar las capacidades de sujetadores y mercados. A pesar de que han nombres que suena intimidante como Hamilton, la unidad, la pendiente, el momento lineal y Laplaciano, estos operadores…
¿Cómo trabajar con un potencial cúbico En la física cuántica, cuando se trabaja con un potencial de caja, usted puede hacer las cosas más simples suponiendo que el cuadro es en realidad un cubo. En otras palabras, L = LX = Ly = Lz. Cuando el cuadro es un cubo, la ecuación de la…
¿Cómo trabajar con vectores propios y eingenvalues En la física cuántica, al trabajar con mercados, es útil saber cómo utilizar vectores propios y valores propios. La aplicación de un operador a un ket puede dar lugar a una nueva ket:Para facilitar las cosas, se puede trabajar con vectores…