¿Cómo encontrar la energía de un oscilador cargada utilizando la teoría de la perturbación
En la física cuántica, cuando se tiene los valores propios exactas para un oscilador cargada en un sistema perturbado, puede encontrar la energía del sistema. Basado en la teoría de la perturbación, la energía corregida del oscilador está dada por
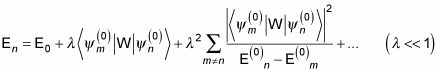
dónde
es el término de perturbación en el hamiltoniano. Es decir, aquí,
Ahora echa un vistazo a la ecuación de energía corregido utilizando
La corrección de primer orden es
que, utilizando
se convierte en
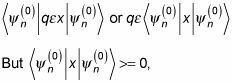
porque ese es el valor esperado de X, y osciladores armónicos pasan tanto tiempo en negativo X territorio como en positivo X territorio - es decir, el valor medio de X es cero. Así que la corrección de primer orden a la energía, dada por la teoría de perturbaciones, es cero.
Está bien, ¿cuál es la corrección de segundo orden a la energía, según lo dado por la teoría de perturbaciones? Aquí está:
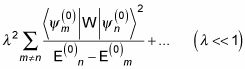
Y por eso
Tienes
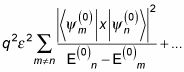
Reparto de esto en términos de sujetadores y mercados, el cambio
hacer la corrección de la energía de segundo orden en esta expresión:
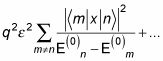
Puede descifrar este paso a paso. En primer lugar, la energía es
Eso hace que averiguar la energía de segundo orden un poco más fácil.
Además, las siguientes expresiones resultan de mantener por un oscilador armónico:
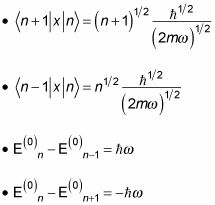
Con estas cuatro ecuaciones, usted está listo para hacer frente a
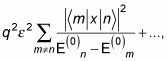
la corrección de segundo orden a la energía. La omisión de términos de mayor potencia, la suma en esta ecuación se convierte en
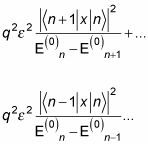
Y sustituyendo por E(0)n - E(0)n + 1 y E(0)n - E(0)n - 1 te dio
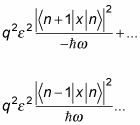
Ahora, sustituyendo en para lt; n + 1 | X | n > Y lt; n - 1 | X | n > Le da
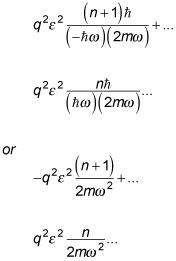
Así que la corrección de segundo orden es
Por lo tanto, de acuerdo con la teoría de la perturbación, la energía del oscilador armónico en el campo eléctrico debe ser
Comparar este resultado a la ecuación anterior para los niveles de energía exactos,
En otras palabras, la teoría de perturbaciones que ha dado el mismo resultado que la respuesta exacta. ¿Cómo es eso de acuerdo?
Por supuesto, no se puede esperar para golpear la misma respuesta cada vez que el uso de la teoría de perturbaciones, pero este resultado es impresionante!
-
Cómo finito es la teoría de cuerdas? -
Cómo determinar estados propios osciladores armónicos de un sistema -
¿Cómo encontrar cualquier estado excitado de un oscilador armónico -
¿Cómo encontrar el nivel de energía de un oscilador armónico: un ejemplo -
¿Cómo encontrar la energía de un sistema perturbado basado en el parámetro de longitud de onda -
¿Cómo encontrar los valores propios y vectores propios para hamiltonianos degenerados
¿Cómo encontrar el estado propio de energía de un oscilador armónico en el espacio posición En la física cuántica, puede utilizar los operadores para determinar el estado propio de energía de un oscilador armónico en el espacio posición. El encanto de la utilización de los operadores la yes que, dado el estado de la tierra, | 0>, los…
¿Cómo encontrar las correcciones de primer orden a los niveles de energía y funciones de onda En la física cuántica, con el fin de encontrar las correcciones de primer orden a los niveles de energía y funciones de onda de un sistema perturbado, En, es necesario calcular E(1)n, al igual queAsique como haces eso? Usted comienza con tres…
¿Cómo encontrar las correcciones de segundo orden a los niveles de energía y funciones de onda En la física cuántica, con el fin de encontrar las correcciones de segundo orden a los niveles de energía y funciones de onda de un sistema perturbado, En, es necesario calcular E(2)n, al igual queAsique como haces eso? Usted comienza con tres…
¿Cómo encontrar la función de onda del estado fundamental de un oscilador cuántico En la física cuántica, se encuentra la función de onda del estado fundamental de un oscilador cuántico, como la que se muestra en la figura, que toma la forma de una curva de Gauss.El estado fundamental de un oscilador armónico mecánica…
Cómo utilizar los operadores de creación y aniquilación de resolver problemas oscilador armónico Creación y aniquilación pueden sonar como grandes tipos make-or-break-del-universo de ideas, pero jugar un papel protagonista en el mundo cuántico cuando se trabaja con osciladores armónicos. Utiliza los operadores de creación y aniquilación…
La medición de la energía de las partículas consolidadas y no consolidadas En la física cuántica, puede resolver para los estados de energía permitidos de una partícula, ya que está obligado, o atrapado, en un pozo de potencial o no está consolidado, tener la energía para escapar.Echa un vistazo a el potencial en la…
Teoría de perturbaciones: el método de la teoría de cuerdas de aproximación Las ecuaciones de la teoría de cuerdas son increíblemente complejo, por lo que a menudo sólo se pueden resolver a través de un método matemático de aproximación llamada teoría de perturbaciones. Este método se utiliza en la mecánica…
La física cuántica y el hamiltoniano Uno de los problemas centrales de la mecánica cuántica es calcular los niveles de energía de un sistema. El operador de la energía, llamada Hamiltoniano, abreviado H, le da la energía total. Encontrar a los niveles de energía de un sistema se…
La teoría de cuerdas y la supersimetría De acuerdo con la teoría de cuerdas, todas las partículas del universo se pueden dividir en dos tipos: bosones y fermiones. La teoría de cuerdas predice que un tipo de conexión, llamado supersimetría, existe entre estos dos tipos de…
La teoría de cuerdas mira a la energía oscura Los recientes descubrimientos en la teoría de cuerdas han permitido la energía oscura a existir dentro de la teoría de cuerdas. Incluso más intrigante que la materia oscura es la energía oscura, que es una energía positiva que parece impregnar…
La teoría de cuerdas: la energía fantasma y universos canallas En la teoría de cuerdas, la hipótesis es que los universos paralelos, separados normalmente no interactúan entre sí, pero algunos enfoques en los últimos años han llamado a esto en tela de juicio. Uno de los más recientes es un documento de…
La teoría de cuerdas unifica masa y energía El trabajo de Einstein condujo a la teoría de que trató de unificar el electromagnetismo y relatividad y es visto por muchos como un precursor de la teoría de cuerdas. La obra más famosa de la vida de Einstein también data de 1905 (un año muy…