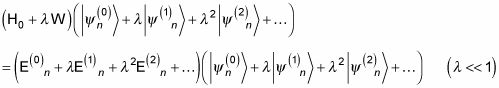¿Cómo encontrar la energía de un sistema perturbado basado en el parámetro de longitud de onda
En la física cuántica, a fin de encontrar la energía de un sistema perturbado, En, que necesita para empezar calculando la función de energía y de las olas de un sistema imperturbable. Se comienza con la energía:
A continuación, añadir la corrección de primer orden a la energía,
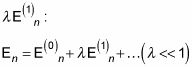
y añadir la corrección de segundo orden a la energía,
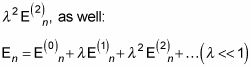
Ahora ¿qué pasa con la función de onda del sistema perturbado,
Comience con la función de onda del sistema no perturbado,
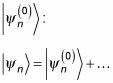
Añadir a que la corrección de primer orden,
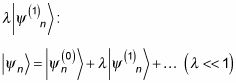
Y a continuación, añadir a que la corrección de segundo orden a la función de onda,
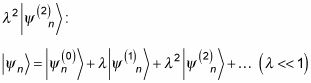
Tenga en cuenta que cuando
se convierte en la energía no perturbada:
y
se convierte en la función de onda imperturbable:
Así que su tarea consiste en calcular E(1)n y E(2)n, al igual que
Entonces, ¿cómo se hace eso en general? Es hora de empezar arrojando un poco de matemática. Usted comienza con tres ecuaciones perturbadas:
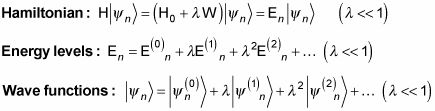
A continuación, combinar estas tres ecuaciones para obtener esta ecuación Jumbo: