Cómo partículas pasan a través de las barreras potenciales que tienen menos energía
Cuando se trabaja con un potencial barrera de altura V0 y el ancho la donde E> V0, esto significa que la partícula tiene suficiente energía para pasar a través de la barrera de potencial y terminan en el X > la región. Esto es lo que el Schr # 246-dinger ecuación se ve como en este caso:
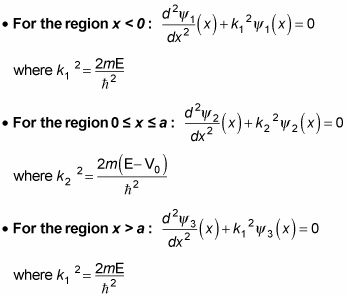
Las soluciones para
son los siguientes:
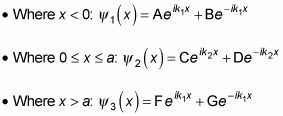
De hecho, porque no hay onda progresiva hacia la izquierda en la X > la región,
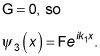
Así que, ¿cómo determinar A, B, C, D, y F? Utiliza las condiciones de continuidad, que trabajan aquí para ser el siguiente:
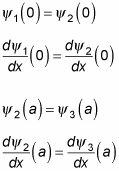
De acuerdo, a partir de estas ecuaciones, se obtiene lo siguiente:
A + B = C + D
ik1(A - B) = ik2(C - D)
Ceik2la + De-ik2la = Feik1la
ik2Ceik2la - ik2De-ik2la = ik1Feik1la
Así que poner todas estas ecuaciones juntos, usted consigue esto para el coeficiente F en términos de A:
Guau. ¿Cuál es el coeficiente de transmisión, T? Bueno, T es
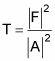
Y esto resulta ser
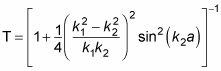
¡Menos mal! Tenga en cuenta que como k1 va a k2, T va a la 1, que es lo que se espera.
Así que ¿qué hay de R, el coeficiente de reflexión? Sin entrar en el álgebra, esto es lo que R es igual a:
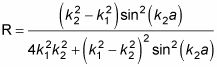
Usted puede ver lo que el E> V0 de densidad de probabilidad,
se parece a la barrera de potencial en la figura.
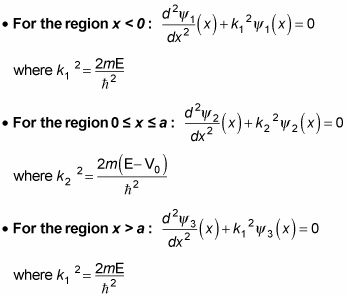
Esto completa la barrera de potencial cuando E> V0.
-
Aplicando la ecuación schr & # 246-dinger en tres dimensiones -
Combinar las soluciones para pequeñas y grandes r r en el schr & # 246-dinger ecuación -
La determinación de los niveles de energía de una partícula en un potencial cuadro -
La determinación de la parte radial de una función de onda -
Encontrar el schr & # 246-dinger ecuación para el átomo de hidrógeno -
Encontrar la función de onda de una partícula en un cuadrado infinito bien con el tiempo
Cómo partículas túnel a través de barreras potenciales que tienen una mayor energía Cuando una partícula no tiene tanta energía como el potencial de una barrera, puede utilizar la ecuación de Schrodinger para encontrar la probabilidad de que el túnel de la voluntad de las partículas a través de la barrera de potencial. Usted…
¿Cómo aplicar el hamiltoniano de un átomo de múltiples electrones neutro Un átomo de múltiples electrones es el sistema de múltiples partículas más frecuente que la física cuántica considera. Se puede aplicar una función de onda de Hamilton a un átomo de múltiples electrones neutro, como se muestra en la…
Cómo desvincular diferentes partículas en ecuaciones linealmente independientes En la física cuántica, se puede desacoplar los sistemas de partículas que se pueden distinguir - es decir, sistemas de identificablemente diferentes partículas - en ecuaciones linealmente independientes. Para ilustrar esto, suponga que tiene un…
Cómo obtener la ecuación 246-dinger schr & # En la física cuántica, la Schr # 246-técnica dinger, que implica la mecánica ondulatoria, utiliza funciones de onda, la mayoría en la base de posición, para reducir las preguntas de la física cuántica a una ecuación diferencial.Werner…
Cómo calcular la ubicación de una partícula aplicando schr & # ecuación de 246-dinger a un paquete de ondas Si usted tiene un número de soluciones a la Schr # 246-dinger ecuación, cualquier combinación lineal de estas soluciones es también una solución. Así que esa es la clave para conseguir una partícula física: Usted agrega varias funciones de…
¿Cómo encontrar la energía total de un sistema de múltiples partículas El hamiltoniano representa la energía total de todas las partículas en un sistema multi-partícula. Puede describir ese sistema en términos de la física cuántica. La siguiente figura muestra un sistema de múltiples partículas donde un número…
Cómo simplificar y dividir la ecuación 246-dinger schr & # hidrógeno En la física cuántica, es posible que necesite para simplificar y dividir la Schr # 246-dinger ecuación de hidrógeno. Aquí está la Schr # 246-dinger ecuación mecánica cuántica habitual para el átomo de hidrógeno:El problema es que usted…
¿Cómo resolver la ecuación 246-dinger schr & # para partículas libres Hay un montón de partículas libres - partículas fuera de cualquier plaza así -en el universo, y la física cuántica tiene algo que decir sobre ellos. El debate se inicia con la Schr # 246-dinger ecuación:Digamos que usted está tratando con…
La medición de la energía de las partículas consolidadas y no consolidadas En la física cuántica, puede resolver para los estados de energía permitidos de una partícula, ya que está obligado, o atrapado, en un pozo de potencial o no está consolidado, tener la energía para escapar.Echa un vistazo a el potencial en la…
Resolución de la función de onda de r utilizando la schr & # ecuación 246-dinger Si su instructor de la física cuántica le pide que resuelva para la función de onda del centro de masas del sistema de electrones / protones en un átomo de hidrógeno, puede hacerlo a través de un Schr # 246-dinger ecuación modificada:Lo que…
Resolución de la función de onda pequeña ry r grande utilizando el schr & # ecuación 246-dinger Su instructor física cuántica puede pedirle que resuelva para la función de onda para una partícula inventada de la masa m en un átomo de hidrógeno. Para hacer esto, puede comenzar utilizando un Schr # 246-dinger ecuación modificada que…
La teoría de cuerdas: acceso a universos paralelos con túnel cuántico En la teoría de cuerdas, una proceso de obtención de un universo a otro sería el uso de la propiedad de túnel cuántico, que es donde se permite que una partícula " salto " de un lugar a otro a través de una barrera.El principio de…