Cómo calcular la aceleración centrípeta de un objeto en órbita

En física, se puede aplicar primera y segunda ley de Newton para calcular la aceleración centrípeta de un objeto en órbita. Primera ley de Newton dice que cuando no hay fuerzas netas, un objeto en movimiento continuará moviéndose uniformemente en línea recta. Para que un objeto se mueva en un círculo, una fuerza tiene que hacer que el cambio en la dirección - esta fuerza se denomina fuerza centrípeta. La fuerza centrípeta se dirige siempre hacia el centro del círculo.

los aceleración centripeta es proporcional a la fuerza centrípeta (obedeciendo segunda ley de Newton). Este es el componente de la aceleración del objeto en la dirección radial (dirigida hacia el centro del círculo), y es la tasa de cambio en la velocidad del objeto como el objeto se mueve en un círculo- la fuerza centrípeta no cambia la magnitud de la velocidad, sólo la dirección.

Puede conectar cantidades angulares, tales como la velocidad angular, a la aceleración centrípeta. Aceleración centrípeta está dada por la siguiente ecuación:

dónde v es la velocidad y r es el radio. La velocidad lineal es bastante fácil para atar a velocidad angular debido

Por lo tanto, se puede reescribir la fórmula aceleración

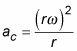
La ecuación de la aceleración centrípeta-se simplifica a

No hay nada que él. La ecuación para la aceleración centrípeta significa que usted puede encontrar la aceleración centrípeta necesaria para mantener un objeto que se mueve en un círculo dado el radio del círculo y la velocidad angular del objeto.

Digamos que usted desea calcular la aceleración centrípeta de la Luna alrededor de la Tierra. Comience con la vieja ecuación

Primero tienes que calcular la velocidad tangencial de la luna en su órbita. Alternativamente, puede utilizar la nueva versión de la ecuación,

Esto es más fácil porque la luna gira alrededor de la Tierra en unos 28 días, por lo que se puede calcular fácilmente la velocidad angular de la luna.

Debido a que la luna hace una órbita completa alrededor de la Tierra en unos 28 días, viaja

alrededor de la Tierra en ese período, por lo que su velocidad angular es

La conversión de los 28 días a segundo le da la siguiente:

Por lo tanto, se obtiene la siguiente velocidad angular:

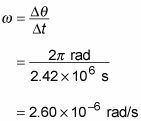
Ahora tiene velocidad angular de la luna,

El radio medio de la órbita de la luna es

por lo que su aceleración centrípeta es

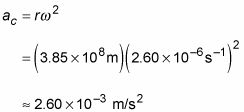
En la ecuación anterior, las unidades de velocidad angular, radianes por segundo, se escriben como s^-1 porque el radián es una sin dimensiones unidad. LA radián es el ángulo barrido por un arco que tiene una longitud igual al radio del círculo. Piense en ello como una parte particular de todo el círculo-, como tal, no tiene dimensiones. Así que cuando usted tiene " radianes por segundo, " puede omitir " radianes, " que te deja con " por segundo ". Otra manera de escribir esto es utilizar el exponente -1, por lo que puede representar radianes por segundo como s^-1.

Sólo por diversión, también se puede encontrar la fuerza necesaria para mantener la Luna dando vueltas en su órbita. Fuerza es igual a masa por aceleración, lo que multiplica la aceleración de la masa de la luna,