Calcular la velocidad necesaria para contrarrestar la gravedad en un bucle

Si conoce el radio de una pista circular, puede utilizar la física para calcular qué tan rápido un objeto necesita moverse para mantenerse en contacto con la pista sin caerse cuando llega a la parte superior del bucle.

Tal vez usted ha visto los deportes extremos en la televisión y se preguntó cómo los ciclistas o patinadores pueden montar en un bucle en una pista e ir boca abajo sin caer al suelo. ¿No debería la gravedad bajarlos? ¿Qué tan rápido es lo que tienen que ir? Las respuestas a estas preguntas circular de movimiento verticales se encuentran en la fuerza centrípeta y la fuerza de la gravedad.

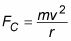
Echa un vistazo a la figura, donde una bola es un bucle alrededor de una pista circular. Una pregunta que puede venir a través de las clases de física introductoria pregunta: " Qué velocidad es necesaria para que la pelota hace que el bucle de seguridad "? El punto crucial es en la parte superior de la pista - si la pelota va a pelar lejos de su pista circular, la parte superior es donde se va a caer. Para responder a la pregunta crucial, usted debe saber qué criterio la pelota debe reunirse para aguantar. Pregúntese, " Cuál es la restricción de que la pelota debe cumplir con el nº 148?;

Para viajar en un bucle, un objeto debe tener una fuerza neta que actúa sobre él que es igual a la fuerza centrípeta que necesita para seguir viajando en un círculo del radio y velocidad dada. En la parte superior de su ruta, como se puede ver en la figura, el balón apenas se mantiene en contacto con la pista. Otros puntos a lo largo de la pista proporcionan fuerza normal debido a la velocidad y el hecho de que la pista es curvo. Si usted quiere saber lo que la velocidad mínima de un objeto debe tener para permanecer en un bucle, que hay que buscar en donde el objeto es apenas en contacto con la pista - en otras palabras, a punto de caerse de su circular camino.

La fuerza normal de la pista se aplica a un objeto en la parte superior es casi cero. La única fuerza que mantiene el objeto en su pista circular es la fuerza de la gravedad, lo que significa que en el ápice, la velocidad del objeto tiene que ser tal que la fuerza centrípeta es igual al peso del objeto para mantenerlo en marcha en un círculo cuyo radio es el mismo que el radio del bucle. Eso significa que si esta es la fuerza necesaria

entonces la fuerza de la gravedad en la parte superior del bucle es

F_g M =_g

Y por eso F_g debe ser igual F_c, puedes escribir

Puede simplificar esta ecuación en la forma siguiente:

La masa de cualquier objeto, tal como una motocicleta o un coche de carreras, que está viajando alrededor de una pista circular cae fuera de la ecuación.

La raíz cuadrada de r veces g es la velocidad mínima de un objeto necesita en la parte superior del bucle con el fin de seguir adelante en un círculo. Cualquier objeto más lento se despega de la pista en la parte superior del bucle (que puede caer de nuevo en el bucle, pero no va a ser después de la pista circular en ese punto). Para un ejemplo práctico, si el bucle de la figura tiene un radio de 20,0 metros, lo rápido que hace la pelota tiene que viajar en la parte superior del bucle con el fin de mantenerse en contacto con la pista? Sólo hay que poner en los números:

En la parte superior de la pista, la pelota de golf tiene que recorrer 14,0 metros por segundo, que es cerca de 31 millas por hora.