Cómo calcular las velocidades de dos objetos con diferentes masas después de una colisión elástica
Cuando una colisión entre dos objetos es elástica, la energía cinética se conserva. En física, la forma más básica de mirar colisiones elásticas es examinar cómo las colisiones funcionan a lo largo de una línea recta. Si ejecuta su auto de choque en el parachoques del coche de un amigo a lo largo de una línea recta, rebotan y la energía cinética se conserva. Pero el comportamiento de los coches depende de la masa de los objetos implicados en la colisión elástica.
He aquí un ejemplo: Usted toma su familia al parque de atracciones de la física para un día de diversión y cálculo, y decide montar los coches de choque. Le hace señas a su familia como a acelerar su 300 kilogramos de coche y conductor de hasta 10,0 metros por segundo. De repente, Bonk! ¿Que pasó? El coche-y-conductor 400 kilogramos en frente de usted había venido a una parada completa, y chocado por detrás del coche elastically- ahora vas a viajar hacia atrás y hacia el otro coche se desplaza hacia adelante. " Interesante, " tu crees. " me pregunto si puedo resolver las velocidades finales de los dos coches de choque ".
Usted sabe que el momento se conservó, y usted sabe que el coche delante de usted se detuvo cuando le pegas, así que si tu coche es de coches 1 y el otro es de coches 2, se obtiene lo siguiente:
m1vF1 + m2vF2 = m1vyo1
Sin embargo, esto no le dice lo que vF1 y vF2 son, porque tiene dos incógnitas y una sola ecuación aquí. No se puede resolver vF1 o vF2 exactamente en este caso, incluso si usted sabe las masas y vyo1. Usted necesita algunas otras ecuaciones que relacionan estas cantidades. ¿Cómo sobre el uso de la conservación de la energía cinética? La colisión era elástica, por lo que la energía cinética se conservó. KE = (1/2)mv2, así que aquí tiene su ecuación para energías cinéticas final e inicial de los dos coches ":
Ahora tienes dos ecuaciones y dos incógnitas, vF1 y vF2, lo que significa que usted puede despejar las incógnitas en cuanto a las masas y vyo1. Usted tiene que cavar a través de una gran cantidad de álgebra aquí porque la segunda ecuación tiene muchas velocidades al cuadrado, pero cuando el polvo se asiente, se obtiene las dos ecuaciones siguientes:
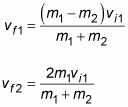
Ahora tu tienes vF1 y vF2 en términos de las masas y vyo1. La conexión de los números que da velocidades finales de los dos coches de choque. Aquí está la velocidad de su coche:
Y aquí está la velocidad final de otro tipo:
Las dos velocidades cuentan toda la historia. Empezaste bajar en 10,0 metros por segundo en un auto de choque de 300 kilogramos, y te encuentras con un auto de choque estacionaria de 400 kilogramos en frente de usted. Suponiendo que la colisión tuvo lugar directamente y el segundo tope del coche despegó en la misma dirección que ibas antes de la colisión, que se recuperó en -1.43 metros por segundo - hacia atrás, porque esta cantidad es negativa y el parachoques del coche delante de usted tenía más masa - y el parachoques del coche delante de usted despegó a una velocidad de 8,57 metros por segundo.
Ahora usted decide volver y recoger en algunos coches de poca luz en un parachoques monstruo coche. ¿Qué sucede si su auto de choque (además del conductor) tiene una masa de 400 kilogramos y que la parte trasera de un coche 300 kilogramos estacionaria? En este caso, se utiliza la ecuación de conservación de la energía cinética, la misma fórmula que se utiliza en el ejemplo anterior. Aquí está lo que su velocidad final sale a:
Velocidad final del pequeño coche viene a
En este caso, usted no rebotar hacia atrás. El, el coche más ligero estacionario se quita después de que lo golpeó, pero no todo su impulso se transfiere al otro coche. ¿Está todavía conserva el impulso? Aquí están sus fórmulas para los ímpetus iniciales y finales:
pyo = m1vyo1
pF = m1vF1 + m2vF2
Poner en los números, aquí está el impulso inicial:
Y aquí está el impulso definitivo:
Los números coinciden, por lo que el impulso se conserva en esta colisión, al igual que es para su colisión con un coche más pesado.
Cómo el principio de conservación de las obras de impulso En física, el principio de conservación del momento establece que cuando se tiene un sistema aislado, sin fuerzas externas, el momento total inicial de los objetos antes de una colisión es igual a la cantidad de movimiento total final de los…
Cómo calcular el poder basado en la fuerza y la velocidad En física, se puede calcular el poder basado en la fuerza y la velocidad. Porque el trabajo es igual a la fuerza por la distancia, se puede escribir la ecuación para la energía de la siguiente manera, suponiendo que la fuerza actúa a lo…
Cómo calcular la energía cinética de un objeto Puede usar la física para calcular la energía cinética de un objeto. Cuando empiece a empujar o tirar de un objeto fijo con una fuerza constante, empieza a mover si la fuerza que se ejerce es mayor que las fuerzas netas que resisten el…
Cómo convertir la energía potencial en energía cinética Cuando un objeto se cae, su energía potencial gravitatoria se cambia a energía cinética. Usted puede usar esta relación para calcular la velocidad de descenso del objeto. Energía potencial gravitatoria de una masa m a la altura del h cerca de…
Cómo determinar si una colisión es elástica o inelástica En la física, las colisiones pueden ser definidos como ya sea elástico o inelástico. Cuando los cuerpos chocan en el mundo real, a veces se aplastan y se deforman hasta cierto punto. La energía para llevar a cabo la deformación proviene de la…
¿Cómo encontrar la velocidad de dos objetos después de la colisión Usted puede utilizar el principio de conservación del momento para medir las características de movimiento, tales como la velocidad. Digamos, por ejemplo, que estás en una expedición de la física y le toca pasar por un lago congelado en un…
¿Cómo encontrar la velocidad de un objeto antes de la colisión En física, el principio de conservación del momento es muy útil cuando no se puede medir la velocidad con un simple cronómetro. Digamos, por ejemplo, que acepta un trabajo de consultoría de un fabricante de municiones que quiere medir la…
Cómo manejar la velocidad como un vector La velocidad es un vector, y como tal, tiene una magnitud y una dirección asociada con él. Supongamos que estás en un automóvil que viaja hacia el este a 88 metros / segundo cuando se empieza a acelerar el norte a 5,0 metros / segundo2 para 10,0…
¿Cómo se relacionan los ángulos entre el centro de masa y los marcos de laboratorio Experimentos de física cuántica tener lugar en el marco de laboratorio, pero usted dispersión cálculos en el marco de centro de masa, por lo que hay que saber cómo relacionar el ángulo entre los dos marcos.He aquí cómo funciona esto: La…
La energía cinética de los objetos en movimiento en problemas de física En física, se puede relacionar la masa, la velocidad de un objeto, y la energía cinética. Por ejemplo, si dos pájaros de diferentes masas están volando a la misma velocidad, se puede calcular cuánto más energía cinética utiliza el más…
Momentum en la física Momentum es la cantidad más importante cuando se trata de manejar las colisiones en la física. Momentum es una cantidad física definida como el producto de la masa multiplicada por la velocidad. Tenga en cuenta la definición dice la velocidad,…
Física: transformar la energía entre las formas cinética y potencial La ley de conservación de la energía es una de las ideas más importantes de la ciencia. Afirma que la energía puede ser transferida o transformado pero nunca crea ni se destruye. Pero, ¿qué es esta cosa que nunca puede ser creada ni destruida?…