Cómo el principio de conservación de las obras de impulso
En física, el principio de conservación del momento establece que cuando se tiene un sistema aislado, sin fuerzas externas, el momento total inicial de los objetos antes de una colisión es igual a la cantidad de movimiento total final de los objetos después de la colisión. En otras palabras,
Es posible que tenga dificultades para hacer frente a la física de impulsos debido a los tiempos cortos y las fuerzas irregulares. Pero con el principio de conservación, elementos que son difíciles de medir - por ejemplo, la fuerza y el tiempo involucrado en un impulso - están fuera de la ecuación por completo. Este principio es simple pero muy útil.
Puede derivar el principio de conservación del momento de las leyes de Newton, lo que sabe sobre los impulsos, y un poco de álgebra.
Dicen que dos pilotos espaciales descuidados están zumbando hacia la escena de un crimen interplanetario. En su afán de llegar a la escena primera, chocan. Durante la colisión, la fuerza media del segundo buque ejerce sobre la primera nave es F12. Aplicando el teorema de impulso-momento a # 8232-el primer barco le ofrece:
Y si la fuerza media ejercida sobre la segunda nave por el primer barco es F21, usted también sabe que
Ahora se agrega estas dos ecuaciones juntas, lo que le da la ecuación resultante:
Distribuir los términos de masa y reorganizar los términos a la derecha hasta que llegue el siguiente:
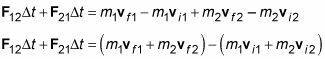
Este es un resultado interesante, porque m1vyo1 + m2vyo2 es el momento total inicial de las dos naves espaciales (p1yo + pyo2) Y m1vF1 + m2vF2 es el impulso final total (p1F + p2F) De las dos naves espaciales. Por lo tanto, se puede escribir la ecuación de la siguiente manera:
Si se escribe el momento total inicial pF y el momento total final como pyo, la ecuación se convierte
¿A donde vas desde aquí? Ambos términos de la izquierda incluyen
para que pueda volver a escribir
como la suma de las fuerzas implicadas,
multiplicado por el cambio en el tiempo:
Si se trabaja con lo que se llama un aislado o sistema cerrado, usted no tiene fuerzas externas que tratar. Tal es el caso en el espacio. Si dos naves espaciales chocan en el espacio, no hay fuerzas externas que son importantes, por lo que por la tercera ley de Newton,
En otras palabras, cuando se tiene un sistema cerrado, se obtiene lo siguiente:
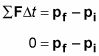
Esto convierte a
pF = pyo
La ecuacion pF = pyo dice que cuando se tiene un sistema aislado, sin fuerzas externas, el momento total inicial antes de una colisión es igual a la cantidad de movimiento total final después de una colisión, que le da el principio de conservación del momento.
Cómo fricción se refiere a la fuerza normal De acuerdo con las leyes de la física, la fuerza de fricción, Ffricción, siempre actúa para oponerse a la fuerza se aplica cuando intenta mover un objeto. La fricción es proporcional a la fuerza con la que un objeto empuja contra la superficie…
¿Cómo afecta el impulso impulso En términos de física, el impulso le dice cuánto el impulso de un objeto cambiará cuando se aplica una fuerza para una cierta cantidad de tiempo. Digamos, por ejemplo, que estás en el billar. Instintivamente, usted sabe lo difícil de…
Cómo calcular el momento angular En física, se puede calcular el momento angular de la misma manera que se calcula la cantidad de movimiento - sólo momento sustituto de inercia de la masa, y la velocidad angular de la velocidad.Imagínate a un niño pequeño en un paseo patio…
Cómo calcular la fuerza de impulso y el impulso En física, se puede utilizar el teorema de impulso-momento de calcular la fuerza basada en el impulso y el impulso. Por ejemplo, se puede relacionar el impulso con que se golpea un objeto para su consiguiente cambio en el momento. De acuerdo con el…
Cómo calcular la energía cinética de un objeto Puede usar la física para calcular la energía cinética de un objeto. Cuando empiece a empujar o tirar de un objeto fijo con una fuerza constante, empieza a mover si la fuerza que se ejerce es mayor que las fuerzas netas que resisten el…
Cómo calcular las velocidades de dos objetos con diferentes masas después de una colisión elástica Cuando una colisión entre dos objetos es elástica, la energía cinética se conserva. En física, la forma más básica de mirar colisiones elásticas es examinar cómo las colisiones funcionan a lo largo de una línea recta. Si ejecuta su auto de…
Cómo determinar si una colisión es elástica o inelástica En la física, las colisiones pueden ser definidos como ya sea elástico o inelástico. Cuando los cuerpos chocan en el mundo real, a veces se aplastan y se deforman hasta cierto punto. La energía para llevar a cabo la deformación proviene de la…
¿Cómo encontrar la velocidad de dos objetos después de la colisión Usted puede utilizar el principio de conservación del momento para medir las características de movimiento, tales como la velocidad. Digamos, por ejemplo, que estás en una expedición de la física y le toca pasar por un lago congelado en un…
¿Cómo encontrar la velocidad de un objeto antes de la colisión En física, el principio de conservación del momento es muy útil cuando no se puede medir la velocidad con un simple cronómetro. Digamos, por ejemplo, que acepta un trabajo de consultoría de un fabricante de municiones que quiere medir la…
Momentum en la física Momentum es la cantidad más importante cuando se trata de manejar las colisiones en la física. Momentum es una cantidad física definida como el producto de la masa multiplicada por la velocidad. Tenga en cuenta la definición dice la velocidad,…
Tercera ley del movimiento de Newton Tercera Ley del Movimiento de Newton es un famoso: " Siempre que un cuerpo ejerce una fuerza sobre un segundo cuerpo, el segundo cuerpo ejerce una fuerza dirigida en sentido opuesto de igual magnitud en el primer cuerpo ". Si eso no suena, prueba…
La segunda ley de Newton: la forma neta fuerza, masa y aceleración afectan el movimiento Primera ley de Newton dice que un objeto permanece en movimiento uniforme a menos que actúe por una fuerza neta. Cuando se aplica una fuerza neta, el objeto se acelera. La segunda ley de Newton se detalla la relación entre la fuerza neta, la masa…