La conservación de la energía cinética
En algunos tipos de colisiones, llamado colisiones elásticas,
la energía cinética y el momento se conservan. ¿Cómo son las colisiones elásticas como? En general, no hay deformación permanente de cualquiera de los objetos de una colisión elástica. Los objetos involucrados inicialmente podría deformarse, pero que salgan inmediatamente de nuevo a su forma original. Aquí están las ecuaciones de conservación de estos factores:KEo = KEFpo P =F
Echa un vistazo a esta idea en acción: Supongamos que estás en un coche cuando usted golpea el coche delante de usted (elásticamente - sin deformación del parachoques está implicado), que comenzó en reposo. Usted sabe que el momento siempre se conserva, y usted sabe que el coche delante de usted se detuvo cuando le pegas, así que si tu coche es un coche de 1 y el otro es un coche de 2, se obtiene la siguiente ecuación:
m1vf1 +m2vf2 = m1vo1
Esta ecuación no puede decir lo que vf1 y vf2 son, porque hay dos incógnitas y una sola ecuación. Usted no puede resolver, ya sea para vF1 o vF2 exactamente en este caso, incluso si usted sabe las masas y vo1. Así que para resolver tanto las velocidades finales, necesita otra ecuación para limitar lo que está pasando aquí. Eso significa que el uso de la conservación de la energía cinética.
La colisión fue uno elástica, por lo que la energía cinética se conserva de hecho. Eso significa que
Con dos ecuaciones y dos incógnitas, vf1 y vf2, puede resolver para aquellas incógnitas en cuanto a las masas y vo1.
Es probable que no se le pedirá para resolver cuestiones de este tipo en las pruebas físicas, ya que, además de ser dos ecuaciones simultáneas, la segunda ecuación tiene una gran cantidad de velocidades al cuadrado en el mismo. Pero es uno que puede ver en la tarea. Cuando se hacen las cuentas, se obtiene
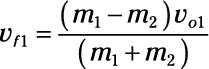
y
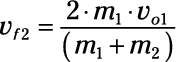
Este es el resultado más importante de lo que se obtiene de los problemas que simplemente utilizan la conservación de momentum- en este tipo de problemas, puede resolver por una sola velocidad final. Aquí, utilizando tanto la conservación del momento y la energía cinética, puede resolver para velocidades finales ambos objetos.
Sin embargo, recuerde que las fórmulas en esta sección el trabajo solamente en el caso especial de una colisión elástica. Además, tendrían que modificarse las fórmulas, si la velocidad inicial del segundo objeto no era cero.
Ejemplo de pregunta
Usted está en un coche que golpea el coche en reposo en frente de usted. Si usted y la masa de su coche es 1,000.0 kg, la masa del coche y el conductor delante de usted es 900,0 kg, y si usted comenzó a los 44 m / s, ¿cuáles son las velocidades finales de los dos coches?
Supongamos que la colisión es elástica y toda la acción sucede en la misma línea que su dirección original de la marcha.
La respuesta correcta es la de que su coche se mueve 2,3 m / s, y el otro coche se mueve 46 m / s.
Usted sabe que esta colisión es elástica y el segundo coche comienza en reposo, por lo que puede utilizar las ecuaciones dadas anteriormente en esta sección. Utilice esta ecuación para encontrar la velocidad final de su coche:
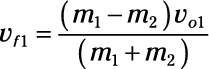
Conecte los números:
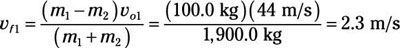
Utilice esta ecuación para encontrar la velocidad final del otro coche:
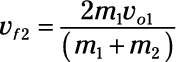
Conecte los números:
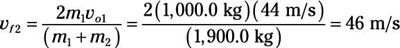
Preguntas de práctica
A 160-g disco de hockey viaja a 60.0 m / s golpea un disco estacionario con la misma masa. ¿Cuáles son las velocidades finales de los discos, ya que la colisión es elástica y que todo movimiento se lleva a cabo en la misma línea?
Usted está conduciendo un auto de choque a los 23 m / s, y chocó con otro auto de choque que está en reposo. Si usted y su coche tiene una masa de 300 kg y la masa del otro coche y el conductor es de 240 kg, lo que son las velocidades finales de los coches?
A continuación se presentan las respuestas a las preguntas de la práctica:
0, 60 m / s
Utilice esta ecuación para encontrar la velocidad final del primer disco:
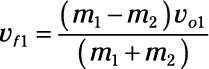
Sustituyendo los números que da:
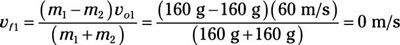
Utilice esta ecuación para encontrar la velocidad final del segundo disco:
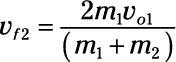
Poner en los números que da:
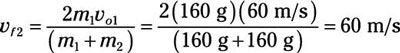
Tenga en cuenta que cuando las masas son los mismos, la primera puck detiene, y el segundo disco se quita con la misma velocidad que el primero tuvo puck.
Usted: 2,6 m / s- el otro coche: 26 m / s
Utilice esta ecuación para encontrar la velocidad final de su coche:
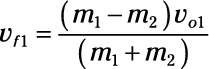
Conecte los números:
Utilice esta ecuación para encontrar la velocidad final del segundo coche:
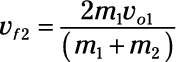
Conecte los números:
Cómo calcular el poder basado en la fuerza y la velocidad En física, se puede calcular el poder basado en la fuerza y la velocidad. Porque el trabajo es igual a la fuerza por la distancia, se puede escribir la ecuación para la energía de la siguiente manera, suponiendo que la fuerza actúa a lo…
Cómo calcular la energía cinética de rotación Si usted pone un montón de trabajo en rotación de un objeto, el objeto comienza a girar. Y cuando un objeto está girando, todas sus piezas se están moviendo, que narra un físico que tiene la energía cinética. Para girar objetos, usted tiene…
Cómo calcular la energía cinética de un objeto Puede usar la física para calcular la energía cinética de un objeto. Cuando empiece a empujar o tirar de un objeto fijo con una fuerza constante, empieza a mover si la fuerza que se ejerce es mayor que las fuerzas netas que resisten el…
Cómo calcular la energía potencial y cinética en un muelle En física, se puede examinar cómo se almacena mucha energía potencial y cinética en una primavera, cuando se comprime o estira. El trabajo que realiza la compresión o estiramiento del muelle debe ir en la energía almacenada en el resorte. Esa…
Cómo calcular las velocidades de dos objetos con diferentes masas después de una colisión elástica Cuando una colisión entre dos objetos es elástica, la energía cinética se conserva. En física, la forma más básica de mirar colisiones elásticas es examinar cómo las colisiones funcionan a lo largo de una línea recta. Si ejecuta su auto de…
Cómo determinar si una colisión es elástica o inelástica En la física, las colisiones pueden ser definidos como ya sea elástico o inelástico. Cuando los cuerpos chocan en el mundo real, a veces se aplastan y se deforman hasta cierto punto. La energía para llevar a cabo la deformación proviene de la…
¿Cómo encontrar la velocidad de dos objetos después de la colisión Usted puede utilizar el principio de conservación del momento para medir las características de movimiento, tales como la velocidad. Digamos, por ejemplo, que estás en una expedición de la física y le toca pasar por un lago congelado en un…
Cómo manejar la velocidad como un vector La velocidad es un vector, y como tal, tiene una magnitud y una dirección asociada con él. Supongamos que estás en un automóvil que viaja hacia el este a 88 metros / segundo cuando se empieza a acelerar el norte a 5,0 metros / segundo2 para 10,0…
¿Cómo se relacionan los ángulos entre el centro de masa y los marcos de laboratorio Experimentos de física cuántica tener lugar en el marco de laboratorio, pero usted dispersión cálculos en el marco de centro de masa, por lo que hay que saber cómo relacionar el ángulo entre los dos marcos.He aquí cómo funciona esto: La…
Momentum en la física Momentum es la cantidad más importante cuando se trata de manejar las colisiones en la física. Momentum es una cantidad física definida como el producto de la masa multiplicada por la velocidad. Tenga en cuenta la definición dice la velocidad,…
Segunda ley del movimiento de Newton Fuerza te salva de la monotonía de todo lo que se mueve a la misma velocidad y dirección siempre. La fuerza puede actuar sobre los objetos, cambiando su dirección y / o velocidad. La relación entre fuerza, masa y aceleración es primaria en…
Problemas de alimentación en la física Cuando se trata de trabajar en la física, que te van a ver los problemas que implican poder, que es la cantidad de trabajo que se realiza en una determinada cantidad de tiempo. Aquí está la ecuación de poder, P:W es igual a la fuerza en la…