¿Cómo se relacionan los ángulos entre el centro de masa y los marcos de laboratorio
Experimentos de física cuántica tener lugar en el marco de laboratorio, pero usted dispersión cálculos en el marco de centro de masa, por lo que hay que saber cómo relacionar el ángulo entre los dos marcos.
He aquí cómo funciona esto: La siguiente figura muestra la dispersión en el marco de laboratorio.
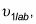
Una partícula que viaja a
incide sobre otra partícula que está en reposo
y le pega. Después de la colisión, la primera partícula se encuentra dispersa en
y la otra partícula se encuentra dispersa en
Ahora, en el marco de centro de masa, el centro de masa está parado y las partículas de la cabeza hacia la otra. Después de chocar, se dirigen de distancia el uno del otro en ángulo
Tienes que ir y venir entre estos dos marcos - la estructura del laboratorio y el recuadro central de masa - por lo que necesita para relacionar las velocidades y ángulos (de una manera no relativista).
Para relacionar los ángulos
se empieza por señalar que se puede conectar
utilizando la velocidad del centro de masa,
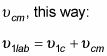
Además, esto es lo que se puede decir acerca de la velocidad de la partícula 1 después de que choca con la partícula 2:
Ahora usted puede encontrar los componentes de estas velocidades:
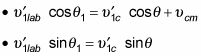
Dividiendo la ecuación en la segunda bala por el uno en el primero le da
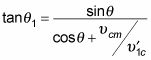
Pero ¿no sería más fácil si pudiera relacionarse
por algo que no involucrar a las velocidades, sólo las masas, como la siguiente?
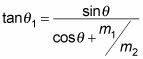
Bueno, se puede. Para ver esto, comenzar con
Y usted puede demostrar que
También puede utilizar la conservación del momento de decir lo que sucede después de la colisión. De hecho, debido a que el centro de masa está parado en el marco de centro de masa, el momento total antes y después de la colisión es cero en ese marco, así:
Por Consiguiente
Y después de la colisión,
Lo que significa que
Además, si la colisión es elástica, la energía cinética se conserva además de impulso, de modo que significa lo siguiente es cierto:
Sustituyendo
en esta ecuación le da
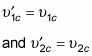
Teniendo en cuenta estas dos ecuaciones, se puede hacer de nuevo
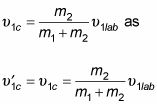
La división de la magnitud de cada lado de
por la magnitud de la ecuación anterior le da
Y porque usted vio antes de que
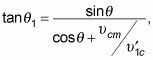
sustitución
en esta ecuación le da al fin
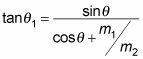
Bueno, eso se relaciona
que es lo que estaba tratando de hacer. Utilizando la relación
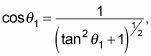
puede volver a escribir
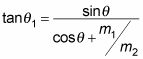
como el siguiente:
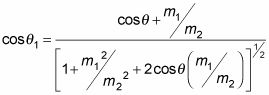
También puede relacionarse
Usted puede demostrar que
que, usando un poco de trig, significa que
Usted ha relacionado los ángulos entre el laboratorio y los marcos de centro de masa.
-
10 ideas importantes en la física -
La conservación de momentum -
La conservación de la energía cinética -
Encontrar la ecuación de energía total para los problemas de partículas libres en tres dimensiones -
Cómo calcular las velocidades de dos objetos con diferentes masas después de una colisión elástica -
Cómo obtener las funciones de onda incidente y dispersos de partículas spinless
Cómo determinar si una colisión es elástica o inelástica En la física, las colisiones pueden ser definidos como ya sea elástico o inelástico. Cuando los cuerpos chocan en el mundo real, a veces se aplastan y se deforman hasta cierto punto. La energía para llevar a cabo la deformación proviene de la…
¿Cómo encontrar los ángulos resultantes en una colisión lab-marco entre las partículas de igual masa Digamos que tienes dos partículas de igual masa que choca en un marco de laboratorio (donde una partícula comienza en reposo). Quiere demostrar que las dos partículas terminan viajando en ángulos rectos con respecto a la otra en el marco del…
¿Cómo encontrar la energía total de un sistema de múltiples partículas El hamiltoniano representa la energía total de todas las partículas en un sistema multi-partícula. Puede describir ese sistema en términos de la física cuántica. La siguiente figura muestra un sistema de múltiples partículas donde un número…
¿Cómo encontrar la velocidad de dos objetos después de la colisión Usted puede utilizar el principio de conservación del momento para medir las características de movimiento, tales como la velocidad. Digamos, por ejemplo, que estás en una expedición de la física y le toca pasar por un lago congelado en un…
¿Cómo encontrar la velocidad de un objeto antes de la colisión En física, el principio de conservación del momento es muy útil cuando no se puede medir la velocidad con un simple cronómetro. Digamos, por ejemplo, que acepta un trabajo de consultoría de un fabricante de municiones que quiere medir la…
Cómo relacionar la amplitud de dispersión y la sección transversal diferencial de partículas spinless La amplitud de dispersión de partículas spinless es crucial para la comprensión de dispersión desde el punto de vista de la física cuántica. Para ver esto, eche un vistazo a las densidades de corriente, Jinc (la densidad de flujo de una…
Cómo simplificar y dividir la ecuación 246-dinger schr & # hidrógeno En la física cuántica, es posible que necesite para simplificar y dividir la Schr # 246-dinger ecuación de hidrógeno. Aquí está la Schr # 246-dinger ecuación mecánica cuántica habitual para el átomo de hidrógeno:El problema es que usted…
¿Cómo traducir secciones transversales entre el centro de masa y los marcos de laboratorio En la física cuántica, una vez que usted se relaciona los ángulos de las partículas dispersas en el marco del laboratorio y el centro de masa del marco, se puede traducir la sección transversal diferencial - el ojo del toro cuando usted está…
Momentum en la física Momentum es la cantidad más importante cuando se trata de manejar las colisiones en la física. Momentum es una cantidad física definida como el producto de la masa multiplicada por la velocidad. Tenga en cuenta la definición dice la velocidad,…
Relacionar impulso y el impulso Resulta que hay una conexión directa entre el impulso y el impulso. Si usted golpea una bola de billar con un taco, taco imparte un cierto impulso a la pelota, haciendo que la pelota para terminar con un impulso particular.¿Cómo se puede…
Resolución de la función de onda de r utilizando la schr & # ecuación 246-dinger Si su instructor de la física cuántica le pide que resuelva para la función de onda del centro de masas del sistema de electrones / protones en un átomo de hidrógeno, puede hacerlo a través de un Schr # 246-dinger ecuación modificada:Lo que…
La teoría de cuerdas y partículas sin masa Un efecto secundario de la creación de una teoría de cuerdas consistente es que tuvo que contener ciertos objetos que no pueden ser llevados a descansar. Debido a que la masa es una medida de un objeto mientras se está en reposo, este tipo de…