La conversión entre ángulos
Estudio en física por lo general comienza con movimiento lineal, que es el movimiento en línea recta. Gran parte de la física se centra en el movimiento angular, sin embargo, que es el movimiento de los objetos en los alrededores de círculos o partes de círculos. Con el fin de estudiar el movimiento angular debe saber cómo medir ese movimiento. Usted utilice radianes, no en metros, y usted tiene que saber lo que eso significa.
Echa un vistazo a la figura, donde se puede ver un ángulo, theta, en un círculo. Supongamos que theta es de 45 grados. ¿Qué es eso en radianes?
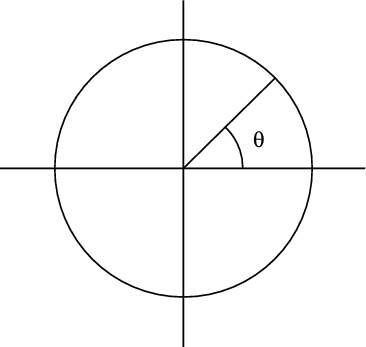
Hay radianes 2pi- en un completo, círculo de 360 grados. Eso significa que para convertir los 45 grados de grados a radianes, multiplique por 2pi- / 360 grados, así:
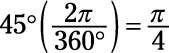
Ángulos medidos en radianes no tienen unidades! Esto se debe a que están expresados como una fracción de 2pi-. A veces se verá ángulos expresados como si radianes eran unidades, pero técnicamente, no lo eres.
El factor de conversión, 2pi- / 360 grados, por lo general se escribe como PI / 180 grados, lo que hace esta conversión:
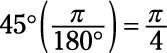
A la inversa, para convertir de radianes a grados, se multiplica por 180 grados / PI. Por ejemplo, la ecuación para convertir PI / 4 en un ángulo se ve así:
Ejemplo de pregunta
Convertir 180 grados en radianes.
La respuesta correcta es PI.
Usa el factor de conversión et- / 180 grados.
Conecte los números:
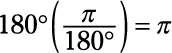
Preguntas de práctica
Lo que es de 23 grados en radianes?
Que es et- / 16 en grados?
A continuación se presentan las respuestas a las preguntas de la práctica:
0,40 radianes
Usa el factor de conversión et- / 180 grados.
Conecte los números:
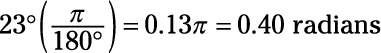
11.2 grados
Usa el factor de conversión de 180 grados / et-.
Conecte los números:
Definir el radián en la trigonometría Introducción de una persona para ángulos es por lo general en términos de grados. Es probable que tenga una buena idea de lo que es un ángulo de 45 grados se parece. E incluso la mayoría de los estudiantes de secundaria saben que un triángulo…
Cómo cambiar grados a radianes El cálculo requerido para el cambio de grados a radianes no es difícil. El cálculo implica un par de trucos, sin embargo, y el formato es importante. Normalmente no escribes las medidas en radianes con valores decimales a menos que haya…
Cómo cambiar radianes a grados Se utiliza la misma proporción básica para cambiar radianes a grados como lo hace para cambiar grados a radianes. El cálculo requerido para el cambio de radianes a grados no es difícil. Por ejemplo, para cambiarradianes a una medida en…
Cómo calcular los ángulos de referencia en grados Despejando el ángulo de referencia en grados es mucho más fácil que tratar de determinar una función trigonométrica del ángulo original. Para calcular la medida (en grados) del ángulo de referencia para cualquier ángulo theta dado, utilizar…
Cómo relacionarse radianes a exploraciones de radar La mayor ventaja de utilizar radianes en lugar de grados es que un radián está directamente relacionado con una longitud - la longitud o distancia alrededor de un círculo, que se llama su circunferencia. Usando radianes es muy útil cuando…
Cómo utilizar radianes para resolver un problema trig Usando radianes es muy útil cuando usted está haciendo aplicaciones de trigonometría que implican la longitud de un arco de un círculo, que es parte de su circunferencia. Esto podría incluir la medición de la barrida de una mano en un reloj o…
Los ángulos positivos y negativos en un círculo unitario El círculo unidad es una plataforma para la descripción de todas las posibles medidas de los ángulos de 0 a 360 grados, todos los negativos de esos ángulos, además de todos los múltiplos de los ángulos positivos y negativos de menos infinito…
Seno y coseno con el álgebra Usted puede aproximar, con bastante precisión, el seno y el coseno de ángulos con un infinito serie, que es la suma de los términos de una secuencia o lista, de los números. Tome en cuenta, sin embargo, que la serie de seno y coseno son exactos…
Ángulo-to-radian conversión en problemas de física En física, es útil saber cómo calcular los ángulos en radianes. Pero en primer lugar, es necesario convertir esos ángulos de grados a radianes. Las siguientes preguntas de práctica que caminan a través del proceso de conversión.Preguntas de…
Velocidad angular Hay análogos de cada cantidad de movimiento lineal (como distancia, velocidad y aceleración) en el movimiento angular, y eso es una de las cosas que hace el movimiento angular más fácil trabajar con después de haber aprendido sobre el…
Conexión de aceleración angular y el desplazamiento angular a la velocidad angular Puede conectar desplazamiento angular, velocidad angular y la aceleración angular. La ecuación correspondiente para el movimiento lineal es vF2 - vo2 = 2como. Sustituyendo omega para v, alfa para la, y para theta s te dio:Utilice esta ecuación…
Conexión de velocidad angular y la aceleración angular al desplazamiento angular Puede conectar velocidad angular, aceleración angular, y el tiempo de desplazamiento angular. Esto es muy similar a la forma en que se conecta velocidad lineal, aceleración lineal, y el tiempo de desplazamiento lineal. Recuerda que se puede…