Cómo utilizar la diferenciación para calcular el volumen máximo de una caja
Uno de los usos más prácticos de la diferenciación es encontrar el valor máximo o mínimo de una función en el mundo real. En el siguiente ejemplo, se calcula el volumen máximo de una caja que no tiene la parte superior y que es ser fabricado a partir de una pieza de 30 pulgadas por 30 pulgadas de cartón cortando y doblándolo como se muestra en la figura.
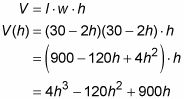
Qué dimensiones producen una caja que tiene el volumen máximo? Matemáticas menudo parece abstracta y poco práctico, pero aquí hay un problema práctico honesto a la bondad. Si un fabricante puede vender cajas más grandes para obtener más dinero, y él o ella está haciendo un millón de cajas, es mejor creer que él o ella va a querer la respuesta exacta a esta pregunta:
Expresar la cosa que quiere maximizada, el volumen, en función de lo desconocido, la altura de la caja (que es la misma que la longitud del corte).
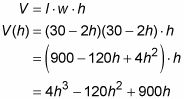
Determine el dominio de su función.
La altura no puede ser negativo o superior a 15 pulgadas (el cartón es de sólo 30 pulgadas de ancho, por lo que la mitad de eso es la altura máxima). Los valores tanto, sensibles para h son 0 # 8804- h # 8804- 15.
Encuentra los números críticos de V(h) En el intervalo abierto (0, 15) mediante el establecimiento de su derivada igual a cero y la solución. Y no se olvide de comprobar los números de donde no está definido del derivado.
Debido a que 15 no se encuentra en el intervalo abierto (0, 15), que no califica como un número crítico. Y debido a que este derivado se define para todos los valores de entrada, no hay números críticos adicionales. Por lo tanto, 5 es el único número crítico.
Evaluar la función en el número crítico, 5, y en los extremos del intervalo, 0 y 15, para localizar máximo de la función.
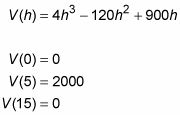
los extremum (cavar esa palabra elegante para máximo o mínimo) Que usted está buscando no suele ocurrir en un punto final, pero puede - por lo que no dejará de evaluar la función en dos puntos extremos del intervalo.
Tienes tu respuesta: una altura de 5 pulgadas produce la caja con el máximo volumen (2000 pulgadas cúbicas). Debido a la longitud y anchura igual 30-2h, una altura de 5 pulgadas da una longitud y anchura de 30 - 2 183- # 5, o 20 pulgadas. Por lo tanto, las dimensiones de la caja deseada son 5 pulgadas por 20 pulgadas por 20 pulgadas.
-
Evaluando las necesidades de tela para fundas de almohada - Área y volumen de proyectos de la casa Cálculo
-
¿Cómo se mide en tres dimensiones -
Encontrar el volumen de un sólido con secciones transversales congruentes -
¿Cómo funciona la integración: es sólo Además de lujo -
Cómo analizar la posición, velocidad y aceleración con la diferenciación
Cómo determinar la máxima aceleración de un objeto en movimiento La aceleración es la derivada de la velocidad. Si una función da la posición de algo como una función del tiempo, a diferenciar la función de posición para obtener la función de la velocidad, y diferenciar la función de velocidad para…
Cómo determinar las velocidades máximas y mínimas de objetos que se mueven Uno de los usos más prácticos de la diferenciación es encontrar los valores máximos o mínimos de una función en el mundo real, por ejemplo, las velocidades máximas y mínimas de un objeto en movimiento.Usted puede pensar en velocidad como la…
¿Cómo encontrar extremos absolutos sobre todo el dominio de una función Una función de absoluta max y absoluta min sobre su todo el dominio son los valores más altos y más bajos (alturas) de la función de cualquier lugar que está definido. Cuando se tiene en cuenta todo el dominio de una función, una función…
¿Cómo encontrar extremos absolutos en un intervalo cerrado Cada función que es continua en un intervalo cerrado tiene un valor máximo absoluto y un valor mínimo absoluto (el extremos absolutos) en ese intervalo - en otras palabras, un punto más alto y más bajo - aunque puede haber un empate en el valor…
¿Cómo encontrar extremos locales con la primera prueba derivada Todos los máximos y mínimos locales en el gráfico de una función - llamada extremos locales - se producen en los puntos críticos de la función (donde la derivada es cero o no definido). (No hay que olvidar, sin embargo, que no todos los puntos…
¿Cómo encontrar los números críticos de una función Todos los extremos locales se producen en los puntos críticos de una función - que es donde la derivada es cero o indefinido (pero no se olvide que los puntos críticos no siempre son extremos locales). Así, el primer paso en la búsqueda de…
Cómo utilizar la diferenciación para calcular la superficie máxima de un corral Encontrar el valor máximo o mínimo de una función en el mundo real es uno de los usos más prácticos de la diferenciación. Por ejemplo, puede que tenga que encontrar el área máxima de un corral, dada una cierta longitud de la esgrima.Digamos…
Cómo utilizar el método Shell para medir el volumen de un sólido los método de shell permite medir el volumen de un sólido mediante la medición del volumen de muchas superficies concéntricas de volumen, llamado " conchas ". Aunque el método de shell funciona sólo para sólidos con secciones transversales…
Militar de aptitud de vuelo: conversiones y equivalentes El vuelo de prueba de Aptitud Militar le preguntará acerca de medidas y conversiones. Necesidad de convertir rápidamente una unidad métrica de una costumbre de Estados Unidos? No hay problema. Estas son algunas de las fórmulas de conversión…
Medición para comprar baldosas de cerámica La compra de baldosas de cerámica para suelos requiere medición y matemáticas. Estimar el número de baldosas de cerámica para comprar mediante el cálculo de la superficie total que va a cubrir y dividiendo ese número por el tamaño de una…
Dimensiones del recinto iguana mínimo No cometa el error de comenzar con un recinto iguana que es demasiado pequeño - iguanas crecen rápidamente. La siguiente tabla muestra las dimensiones del recinto mínimos necesarios con base en el tamaño medio de longitud hocico-cloaca (LHC) y…
Tamaños Ronda-mantel para su recepción de boda Cambiar el aspecto de toda la recepción de la boda simplemente eligiendo un mantel palabra de longitud. Pero, ¿qué tamaño mantel cubrirá esas piernas desagradables, de aspecto industrial de una mesa de banquete normalmente ronda? He aquí una…