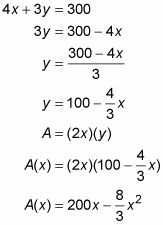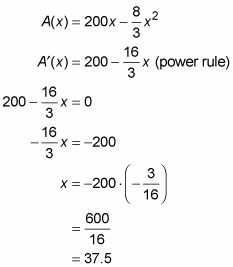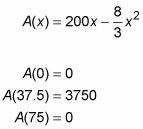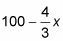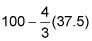Cómo utilizar la diferenciación para calcular la superficie máxima de un corral
Encontrar el valor máximo o mínimo de una función en el mundo real es uno de los usos más prácticos de la diferenciación. Por ejemplo, puede que tenga que encontrar el área máxima de un corral, dada una cierta longitud de la esgrima.
Digamos que un ranchero puede darse el lujo de 300 pies de cercado para construir un corral que se divide en dos rectángulos iguales. Qué dimensiones maximizará el área del corral? El ranchero quiere dar a sus animales tanto espacio como sea posible mediante el uso de la longitud de la esgrima que puede permitirse. Como todos los hombres de negocios, que quiere la mayoría de la explosión para su buck:
Expresar lo que desea maximizado, la zona, en función de las dos incógnitas, X y y.

LA = l # 183- w
= (2X) (y)
Debido a que el área es una función de dos variables, Paso 1 tiene dos sub-etapas adicionales.
Use la información dada a relacionar las dos incógnitas entre sí.
La esgrima es utilizado por siete secciones, por lo tanto
300 = X + X + X + X + y + y + y
300 = 4X + 3y
Resuelva esta ecuación para y, y enchufe el resultado en el y en la ecuación del Paso 1. Esto le da lo que necesita - una función de una variable.
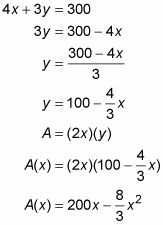
Determinar el dominio de la función.
No se puede tener una longitud negativo de cerca, por lo que X no puede ser negativo, y el más X puede ser es 300 dividido por 4 o 75. De este modo, el dominio es 0 # 8804- X # 8804- 75.
Encuentra los números críticos de LA(X) En el intervalo abierto (0, 75) mediante el establecimiento de su derivada igual a cero y la solución.
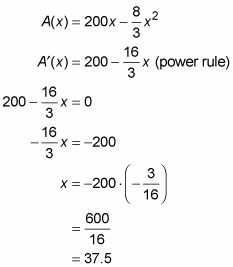
Porque LA# 8242- se define para todos X-valores, 37.5 es el único número crítico.
Evaluar la función en el número crítico, 37.5, y en los extremos del intervalo, 0 y 75.
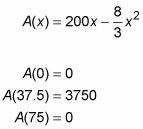
Tenga en cuenta que la evaluación de una función en los puntos finales de un intervalo es un paso normal en la búsqueda de un valor extremo absoluto en el intervalo. Sin embargo, podría haber saltado este paso aquí habías notado que LA(X) Es una parábola al revés y que, por tanto, su punto más alto debe ser más alto que sea punto final.
El valor máximo en el intervalo es de 3.750, y por lo tanto, una X-valor de 37,5 pies maximiza el área del corral. La longitud es de 2X, o 75 pies. El ancho es y, que es igual
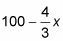
La conexión de 37.5 le da
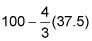
o 50 pies. Así que el ganadero va a construir una de 75 pies por 50 pies de corral con una superficie de 3750 pies cuadrados.
Esta es una situación del mundo real donde vale la pena hacer los cálculos. ¿Había el ranchero no resuelto este problema, él probablemente habría construido una, corral más pequeño inferior. Mucha gente sabe que un cuadrado frecuencia maximiza el área (este sería el caso, por ejemplo, en un problema de corral similares donde no hay valla divisoria en medio del corral). Por lo tanto, el ganadero podría haber pensado que debía construir una plaza de corral o, quizás un corral rectangular formado por dos cuadrados. Estos dos corrales tendrían áreas totales de, respectivamente, 3600 pies cuadrados y 3673 pies cuadrados. Por supuesto, el área perdida no es sustancial en cualquiera de los casos, pero ¿por qué calambre sus animales incluso un poco sin razón? Y, en otros problemas, no encontrar una máxima exacta o mínimo puede tener mucho más consecuencias significativas.
Sobre el autor
 ¿Cómo encontrar extremos absolutos sobre todo el dominio de una función
¿Cómo encontrar extremos absolutos sobre todo el dominio de una función Una función de absoluta max y absoluta min sobre su todo el dominio son los valores más altos y más bajos (alturas) de la función de cualquier lugar que está definido. Cuando se tiene en cuenta todo el dominio de una función, una función…
 ¿Cómo encontrar extremos absolutos en un intervalo cerrado
¿Cómo encontrar extremos absolutos en un intervalo cerrado Cada función que es continua en un intervalo cerrado tiene un valor máximo absoluto y un valor mínimo absoluto (el extremos absolutos) en ese intervalo - en otras palabras, un punto más alto y más bajo - aunque puede haber un empate en el valor…
 ¿Cómo encontrar el valor medio de una función con el teorema del valor medio para integrales
¿Cómo encontrar el valor medio de una función con el teorema del valor medio para integrales Usted puede encontrar el valor medio de una función en un intervalo cerrado usando el teorema del valor medio para integrales. La mejor manera de entender el teorema del valor medio es con un diagrama - echa un vistazo a continuación.El gráfico…
 ¿Cómo encontrar el valor medio con el teorema del valor medio para integrales
¿Cómo encontrar el valor medio con el teorema del valor medio para integrales Usted puede encontrar el valor medio de una función en un intervalo cerrado usando el teorema del valor medio para integrales. La mejor manera de entender el teorema del valor medio para integrales es con un diagrama - mira el siguiente figura.El…
 Cómo identificar el mínimo y máximo en parábolas verticales
Cómo identificar el mínimo y máximo en parábolas verticales Parábolas verticales dan una pieza importante de información: Cuando la parábola se abre hacia arriba, el vértice es el punto más bajo en el gráfico - llamado el mínimo, o min. Cuando la parábola se abre hacia abajo, el vértice es el punto…
 Cómo utilizar la diferenciación para calcular el volumen máximo de una caja
Cómo utilizar la diferenciación para calcular el volumen máximo de una caja Uno de los usos más prácticos de la diferenciación es encontrar el valor máximo o mínimo de una función en el mundo real. En el siguiente ejemplo, se calcula el volumen máximo de una caja que no tiene la parte superior y que es ser fabricado…
 ¿Cómo encontrar el área de un triángulo para sss según la fórmula de la garza
¿Cómo encontrar el área de un triángulo para sss según la fórmula de la garza Puede utilizar la fórmula de Herón para calcular el área del triángulo, incluso si sólo se sabe de los lados del triángulo y no cualquiera de los ángulos (que se llama SSS, o de lado de lado a lado, en términos de trigonometría). La…
 Radio, diámetro, circunferencia, y el área de círculos
Radio, diámetro, circunferencia, y el área de círculos LA círculo es una figura geométrica que necesita sólo dos piezas que lo identifican y clasifican: su centro (o medio) y su radio (la distancia desde el centro hasta cualquier punto en el círculo). Después de elegir un punto para ser el centro…
 ¿Cómo resolver problemas geométricos en el ASVAB
¿Cómo resolver problemas geométricos en el ASVAB Problemas geométricos en el ASVAB requieren que calcular el volumen, perímetro, área, circunferencia, diámetro, y así sucesivamente de varias formas geométricas. Estos problemas no son muy difíciles con un poco de conocimiento de algunas…
 Las leyes de zonificación y otros reglamentos de construcción
Las leyes de zonificación y otros reglamentos de construcción A pesar del hecho de que Estados Unidos tiene leyes muy fuertes que protegen los derechos de la propiedad privada, en prácticamente todas las partes del país hay leyes que limitan lo que se puede construir en esa misma propiedad privada.De todas…
 Estimación de la cantidad de pintura para comprar
Estimación de la cantidad de pintura para comprar Antes de comenzar a pintar de su casa interiores paredes, techos, carpintería, puertas, o ventanas, es necesario estimar la cantidad de pintura que va a utilizar. Las estimaciones requieren cálculos específicos para cada superficie que desea…
 ¿Cuántas cabras debe llegar?
¿Cuántas cabras debe llegar? Antes de traer a casa ningún cabras para complementar su estilo de vida verde, usted tiene que determinar el número de cabras que realmente necesita. Uno de los mayores errores nuevos agricultores cabra hacen es conseguir demasiadas cabras. Usted…