Cómo determinar la máxima aceleración de un objeto en movimiento
La aceleración es la derivada de la velocidad. Si una función da la posición de algo como una función del tiempo, a diferenciar la función de posición para obtener la función de la velocidad, y diferenciar la función de velocidad para obtener la función de aceleración. Dicho de una manera diferente pero equivalente, la primera derivada de la posición es la velocidad, y la segunda derivada de la posición es la aceleración.
He aquí un ejemplo. Un yo-yo se mueve hacia arriba y hacia abajo. Su altura sobre el suelo, como una función del tiempo, viene dada por la función de H(t) = t3 - 6t2 + 5t + 30, donde t es en segundos y H(t) Es en pulgadas. A t = 0, es 30 pulgadas sobre el suelo, y después de 4 segundos, es a una altura de 18 pulgadas, como se muestra en el primer gráfico en la figura.
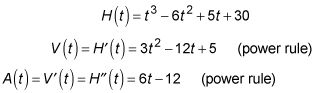
Velocity, V(t), Es la derivada de la posición (altura, en este problema), y la aceleración, LA(t), Es la derivada de la velocidad. Por lo tanto:
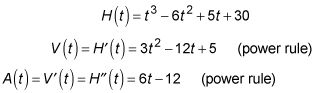
La gráfica de la función de aceleración en la parte inferior de la figura es una línea simple, LA(t) = 6t - 12.
Es fácil ver que la aceleración del yo-yo va de un mínimo de
a t = 0 segundos a un máximo de
a t = 4 segundos, y que la aceleración es cero en t = 2 cuando el yo-yo llegue a su velocidad mínima (y la velocidad máxima). Cuando la aceleración es negativo - en el intervalo [0, 2) - que significa que la velocidad es decreciente. Cuando la aceleración es positivo - en el intervalo (2, 4] - la velocidad es creciente.
Un objeto se está acelerando (lo que llamamos "aceleración" en el habla cotidiana) siempre que la velocidad y la aceleración de cálculo son ambos positivos o ambos negativos. Y un objeto se está desacelerando ("desaceleración" en el habla cotidiana) cuando la velocidad y la aceleración de cálculo son de signos opuestos.
Mira todos los tres gráficos de la figura de nuevo. De t = 0 a alrededor de t = 0.47, la velocidad es positiva y la aceleración es negativa, por lo que el yo-yo está desacelerando mientras se mueve hacia arriba (hasta su velocidad se hace cero y alcanza su altura máxima). En la llanura Inglés, el yo-yo está desacelerando de 0 a aproximadamente 0,47 segundos. El mayor deceleración se produce en t = 0 cuando la desaceleración es
(muestra el gráfico negativo 12, pero se puede pensar que es positivo 12, ya que se está desacelerando, lo consigue?)
Desde aproximadamente t = 0,47 a t = 2, tanto la velocidad y la aceleración son negativos, por lo que el yo-yo está acelerando mientras se mueve hacia abajo. De t = 2 a alrededor de t = 3.53, la velocidad es negativa y la aceleración es positiva, por lo que el yo-yo se desacelera de nuevo a medida que continúa hacia abajo (hasta que toque fondo en su altura más baja). Por último, desde alrededor t = 3.53 a t = 4, tanto la velocidad y la aceleración son positivos, por lo que el yo-yo está acelerando de nuevo. El yo-yo alcanza su mayor aceleración del
a t = 4 segundos.
-
Cálculo: cómo resolver los problemas de diferenciación -
Cómo analizar la posición, velocidad y aceleración con la diferenciación -
Cómo determinar las velocidades máximas y mínimas de objetos que se mueven -
Aceleración en problemas de física -
La aceleración angular en problemas de física -
Cálculo de la aceleración tangencial en una curva
Cálculo de la aceleración de un objeto en movimiento armónico simple En física, se puede calcular la aceleración de un objeto en movimiento armónico simple ya que se mueve en un círculo- todo lo que necesitas saber es radio de la trayectoria del objeto y la velocidad angular.Usted puede encontrar el…
Aceleración centripeta Con el fin de mantener un objeto dando vueltas en un círculo, ese objeto debe ser tirado hacia el centro del círculo. Echa un vistazo a la luna rodeando la Tierra en la siguiente figura. La Luna se acelera hacia la Tierra a lo largo de un radio de…
Conexión de aceleración angular y el desplazamiento angular a la velocidad angular Puede conectar desplazamiento angular, velocidad angular y la aceleración angular. La ecuación correspondiente para el movimiento lineal es vF2 - vo2 = 2como. Sustituyendo omega para v, alfa para la, y para theta s te dio:Utilice esta ecuación…
Conexión de aceleración, tiempo, y el desplazamiento en problemas de física Usted sabe que usted puede relacionarse con la velocidad de desplazamiento y el tiempo. Y usted sabe que usted puede relacionarse velocidad y tiempo para obtener la aceleración. También puede relacionarse desplazamiento con la aceleración y el…
Conexión de velocidad angular y la aceleración angular al desplazamiento angular Puede conectar velocidad angular, aceleración angular, y el tiempo de desplazamiento angular. Esto es muy similar a la forma en que se conecta velocidad lineal, aceleración lineal, y el tiempo de desplazamiento lineal. Recuerda que se puede…
Encontrar a distancia utilizando la velocidad inicial, la hora y la aceleración En una ecuación de la física, dada la velocidad inicial, la hora y la aceleración, usted puede encontrar el desplazamiento de un objeto. He aquí un ejemplo: Ahí lo tienes, el héroe del Tour de Francia, dispuesto a dar una demostración de sus…
Cómo angular obras de aceleración Si los puntos de velocidad de vector angular fuera del plano de rotación de una rueda, puede usar la física para determinar lo que sucede cuando los cambios de velocidad angular - cuando la rueda se acelera o ralentiza. Un cambio en la velocidad…
Cómo acción centrípeta mantiene un objeto que se mueve en un círculo De acuerdo con las leyes de la física, con el fin de mantener un objeto en movimiento en movimiento circular, su velocidad cambia constantemente de dirección. Siempre que los cambios de velocidad, que tienen la aceleración. Específicamente,…
Cómo aceleración centrípeta mantiene un objeto que se mueve en un círculo constante En física, cuando un objeto se desplaza en movimiento circular uniforme, su velocidad es constante, lo que significa que la magnitud de la velocidad del objeto no cambia. Por lo tanto, la aceleración no puede tener ningún componente en la misma…
Cómo positiva y aceleración negativa se refieren a la velocidad y la velocidad En física, el signo de la aceleración de un objeto depende de su dirección. Si vas más despacio a una parada completa en un coche, por ejemplo, y su velocidad original era positiva y su velocidad final fue de 0, por lo que su aceleración es…
Cómo calcular la aceleración En términos de física, aceleración, la, es la cantidad en la que los cambios de velocidad en una determinada cantidad de tiempo. Teniendo en cuenta las velocidades iniciales y finales, vyo y vF, y los tiempos iniciales y finales sobre las que los…
Cómo calcular la aceleración centrípeta de un objeto en órbita En física, se puede aplicar primera y segunda ley de Newton para calcular la aceleración centrípeta de un objeto en órbita. Primera ley de Newton dice que cuando no hay fuerzas netas, un objeto en movimiento continuará moviéndose uniformemente…