¿Cómo encontrar extremos locales con la primera prueba derivada

Todos los máximos y mínimos locales en el gráfico de una función - llamada extremos locales - se producen en los puntos críticos de la función (donde la derivada es cero o no definido). (No hay que olvidar, sin embargo, que no todos los puntos críticos son necesariamente extremos locales.)

El primer paso en la búsqueda de extremos locales de una función es encontrar los números críticos (el X-valores de los puntos críticos). A continuación, utiliza la primera derivada. Esta prueba se basa en las ideas del premio Nobel de calibre que a medida que se pasa de la parte superior de una colina, primero tienes que subir y luego bajar, y que cuando se conduce dentro y fuera de un valle, hay que bajar y luego arriba. Este material cálculo es bastante increíble, ¿eh?

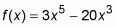
La figura muestra la gráfica de

Para encontrar los números críticos de esta función, esto es lo que haces.

1. Encuentra la primera derivada de F usando la regla de la potencia.

   

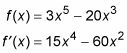
2. Establezca la igualdad derivada a cero y resolver para X.

   

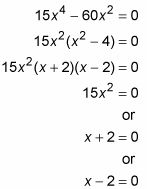
   X = 0, -2, o 2.

   Estas tres X-Los valores son los números críticos de f. Números críticos adicionales podrían existir si la primera derivada se indefinido en algún X-valores, pero debido a que el derivado de

   

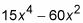
   está definida para todos los valores de entrada, el conjunto solución anterior, 0, -2 y 2, es la lista completa de los números críticos. Debido a que el derivado (y la pendiente) de F es igual a cero en estos tres números críticos, la curva tiene tangentes horizontales en estos números.

Ahora que tienes la lista de los números críticos, es necesario determinar si los picos o valles o ni se producen en los X-los valores. Usted puede hacer esto con la primera derivada. Así es cómo:

1. Tome una línea de números y poner los números críticos que ha encontrado: 0, -2 y 2.

   

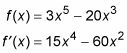
   Se divide esta línea número en cuatro regiones: a la izquierda de -2, desde -2 a 0, de 0 a 2, y a la derecha de 2.

2. Elija un valor de cada región, conéctelo a la primera derivada, y tenga en cuenta si el resultado es positivo o negativo.

   Para este ejemplo, puede utilizar los números -3, -1, 1 y 3 para poner a prueba las regiones.

   

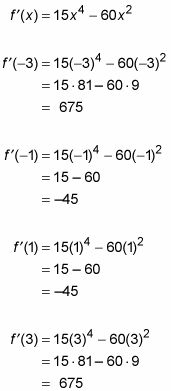
   Estos cuatro resultados son, respectivamente, positivo, negativo, negativo y positivo.

3. Lleve a su línea de números, marque cada región con el signo positivo o negativo apropiada, e indicar que la función es creciente y decreciente.

   Está aumentando donde la derivada es positiva, y la disminución de donde la derivada es negativa. Ycompararlos es un llamado gráfico de señal para la función.

   

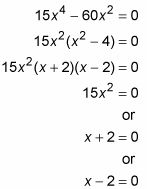
   Esta cifra simplemente te dice lo que ya sabes si has mirado la gráfica de F - que la función sube hasta -2, por debajo de -2 a 0, más abajo de 0 a 2, y de nuevo a partir de 2 sucesivamente.

   Ahora, aquí está la ciencia de cohetes. Los interruptores de función de creciente a decreciente en -2- en otras palabras, que suben a -2 y luego hacia abajo. Así, a -2, usted tiene una colina o un máximo local. A la inversa, ya que la función cambia de disminuir a aumentar a los 2, usted tiene un valle allí o un mínimo local. Y debido a que el signo de la primera derivada no cambia en cero, no hay ni un min ni un máximo en ese X-valor.

4. Obtener los valores de la función (en otras palabras, las alturas) de estos dos extremos locales conectando el X-valores en la función original.

   

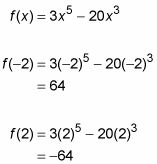
   Así, el máximo local está situado en (-2, 64), y el min local es en (2, -64). Ya terminaste.

Para usar la primera derivada para la prueba de un extremo local en un número crítico particular, la función debe ser continuo a eso X-valor.