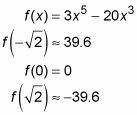Cómo localizar intervalos de puntos de inflexión y concavidad
Puede localizar la concavidad de una función (donde una función es cóncava hacia arriba o hacia abajo) y los puntos de inflexión (donde los interruptores concavidad de positivo a negativo o vice versa) en unos sencillos pasos. El siguiente método muestra cómo encontrar los intervalos de concavidad y los puntos de inflexión de
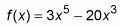
Encuentra la segunda derivada de f.
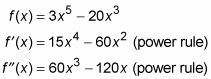
Establezca la segunda derivada igual a cero y resolver.
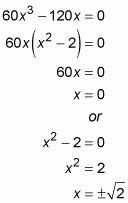
Determinar si la segunda derivada es indefinido para cualquier X-los valores.

Los pasos 2 y 3 le dan lo que podríamos llamar " números críticos segundos derivados " de F porque son análogos a los números críticos de F que se encuentra utilizando la primera derivada. Pero este conjunto de números no tiene nombre especial. En cualquier caso, lo importante es saber que esta lista se compone de los ceros de F# 8242- # 8242- más cualquier X-valores donde F# 8242- # 8242- es indefinido.
Trazar estos números en una recta numérica y poner a prueba las regiones con segundo derivado.
Utilice -2, -1, 1, y 2 como números de prueba.
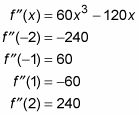
Debido a -2 se encuentra en la izquierda, la mayoría región en la recta numérica de abajo, y debido a que la segunda derivada en -2 iguales negativo 240, esa región que sufre es un signo negativo en la figura siguiente, y así sucesivamente para las otras tres regiones.
Un segundo gráfico señal derivada.
Un signo positivo en este gráfico muestra que usted dice que la función es cóncava hacia arriba en ese intervalo- un medio de signos negativos cóncava hacia abajo. La función tiene un punto de inflexión (por lo general) en cualquier X-valor donde los signos cambian de positivo a negativo o viceversa vicio.
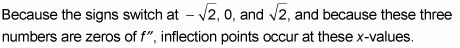
(Si usted recibe un problema en el que cambian los signos en un número donde la segunda derivada es indefinido, usted tiene que comprobar una cosa más antes de concluir que hay un punto de inflexión allí. Un punto de inflexión existe en un determinado X-valor sólo si hay una línea tangente a la función en ese número. Este es el caso donde existe la primera derivada, o cuando hay una tangente vertical.)
Conecte estos tres X-valores en F para obtener los valores de la función de los tres puntos de inflexión.
Un gráfico que muestra los puntos de inflexión y los intervalos de concavidad.
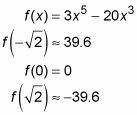
La raíz cuadrada de dos es igual a alrededor de 1,4, por lo que hay puntos de inflexión en alrededor (-1,4, 39,6), (0, 0), y aproximadamente (1.4, -39.6).
Sobre el autor
 Multiplicación y división con números negativos
Multiplicación y división con números negativos Multiplicación y división con números negativos es prácticamente lo mismo que con los números positivos. La presencia de uno o más signos menos (-) no cambia la parte numérica de la respuesta. La única pregunta es si el signo es positivo o…
 Cartesiano Parcela puntos de coordenadas en un gráfico cartesiano
Cartesiano Parcela puntos de coordenadas en un gráfico cartesiano Cuando la gente habla de matemáticas utilizando un gráfico, que están por lo general se refiere a un gráfico cartesiano (también llamado el sistema de coordenadas cartesianas). La siguiente figura muestra un ejemplo de una gráfica…
 Cómo gráficas de derivados difieren de gráficas de funciones
Cómo gráficas de derivados difieren de gráficas de funciones Cuando se empieza a observar las gráficas de los derivados, puede caducar fácilmente en pensar en ellos como funciones regulares - pero no lo son. Afortunadamente, usted puede aprender mucho acerca de las funciones y sus derivados mirando su lado…
 Cómo analizar la posición, velocidad y aceleración con la diferenciación
Cómo analizar la posición, velocidad y aceleración con la diferenciación Cada vez que te metes en tu coche, ser testigo de primera mano la diferenciación. Su velocidad es la primera derivada de su posición. Y cuando se pisa el acelerador o el freno - acelerar o desacelerar - experimenta una segunda derivada.Si una…
 Cómo determinar el costo marginal, el ingreso marginal y el beneficio marginal en la economía
Cómo determinar el costo marginal, el ingreso marginal y el beneficio marginal en la economía El costo marginal, el ingreso marginal y beneficio marginal todos implican la cantidad de una función sube (o hacia abajo) a medida que avanza más de 1 hacia la derecha - esto es muy similar a la forma en que las obras de aproximación…
 Cómo determinar la máxima aceleración de un objeto en movimiento
Cómo determinar la máxima aceleración de un objeto en movimiento La aceleración es la derivada de la velocidad. Si una función da la posición de algo como una función del tiempo, a diferenciar la función de posición para obtener la función de la velocidad, y diferenciar la función de velocidad para…
 ¿Cómo encontrar derivados de alto orden
¿Cómo encontrar derivados de alto orden Encontrar un segundo, tercero, cuarto, o superior derivado es increíblemente simple. La segunda derivada de una función es simplemente la derivada de su primera derivada. La tercera derivada es la derivada de la segunda derivada, el cuarto…
 ¿Cómo encontrar extremos locales con la primera prueba derivada
¿Cómo encontrar extremos locales con la primera prueba derivada Todos los máximos y mínimos locales en el gráfico de una función - llamada extremos locales - se producen en los puntos críticos de la función (donde la derivada es cero o no definido). (No hay que olvidar, sin embargo, que no todos los puntos…
 ¿Cómo encontrar los números críticos de una función
¿Cómo encontrar los números críticos de una función Todos los extremos locales se producen en los puntos críticos de una función - que es donde la derivada es cero o indefinido (pero no se olvide que los puntos críticos no siempre son extremos locales). Así, el primer paso en la búsqueda de…
 ¿Cómo encontrar las líneas tangentes de una parábola que pasan por un punto determinado
¿Cómo encontrar las líneas tangentes de una parábola que pasan por un punto determinado ¿Alguna vez quiso determinar la ubicación de una línea a través de un punto dado que es tangente a una curva dada? Por supuesto que tienes! He aquí cómo lo haces.Determinar los puntos de tangencia de las líneas por el punto (1, -1) que son…
 Cómo graficar una función tangente
Cómo graficar una función tangente La función tangente tiene una gráfica de los padres al igual que cualquier otra función. Utilizando la gráfica de esta función, se puede hacer el mismo tipo de transformación que se aplica a la gráfica de los padres de cualquier función. La…
 ¿Cómo saber cuando un derivado no existe
¿Cómo saber cuando un derivado no existe Hay tres situaciones en las que un derivado de falla de existir. La derivada de una función en un punto dado es la pendiente de la recta tangente en ese punto. Por lo tanto, si no se puede trazar una línea tangente, no hay derivada - que sucede en…
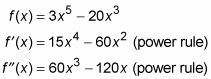
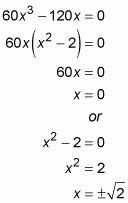

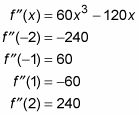
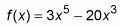 Un segundo gráfico señal derivada.
Un segundo gráfico señal derivada.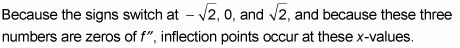
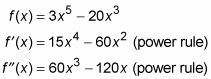 Un gráfico que muestra los puntos de inflexión y los intervalos de concavidad.
Un gráfico que muestra los puntos de inflexión y los intervalos de concavidad.