Cómo graficar la inversa de una función

categoría Educación y lenguas / Matemáticas / Cálculo

Si se le pregunta para representar gráficamente la inversa de una función, puede hacerlo recordando un hecho: una función y su inversa se reflejan sobre la línea y = X. Esta línea pasa por el origen y tiene una pendiente de 1.

Cuando se le pide que dibuje una función y su inversa, usted puede optar por dibujar esta línea en como puntos de línea de esta manera, actúa como un gran espejo, y se puede ver, literalmente, los puntos de la función que reflejan sobre la línea para convertirse en los puntos de función inversa. Reflexionando sobre esa línea cambia el X y el y y te da una manera gráfica para encontrar la inversa sin trazar toneladas de puntos.

La mejor manera de entender este concepto es verlo en acción. Por ejemplo, digamos que usted sabe que estas dos funciones son inversas entre sí:

image0.jpg

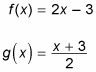
Para ver cómo X y y cambiar de lugar, siga estos pasos:

  1. Tome un número (cualquiera que desee) y conectarlo a la primera función dada.

    Digamos que usted elija -4. Al evaluar F(-4), Se obtiene -11. Como punto, esto se escribe (-4, -11).

  2. Tome el valor del paso 1 y conectarlo a la otra función.

    En este caso, es necesario encontrar g(-11). Cuando lo haga, se obtiene -4 viceversa. Como punto, esto es (-11, -4). Whoa!

Esto funciona con alguna número y con alguna función y su inversa: El punto (una B) En la función se convierte en el punto (b, a) En su inverso. Pero no dejes que te engañe la terminología. Porque son todavía puntos, les graficar la misma manera que siempre has sido puntos gráficas.

Todo el dominio y rango de swap lugares de una función a su inversa. Por ejemplo, a sabiendas de que sólo algunos puntos de la función dada F(X) = 2X - 3 incluyen (-4, -11), (-2 -7,) y (0, -3), ustedes saben automáticamente que los puntos de la inversa g(X) Será (-11, -4), (-7 -2,), y (-3, 0).

Así que si te piden para graficar una función y su inversa, todo lo que tienes que hacer es gráfico de la función y luego cambiar todo X y y valores en cada punto para representar gráficamente la inversa. Basta con mirar a todos esos valores lugares de la conmutación F(XFunción) a su inversa g(X) (Y viceversa), que se refleja sobre la línea y = X.

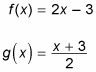
image1.jpg

Ahora puede representar gráficamente la función F(X) = 3X - 2 y su inversa sin siquiera saber lo que su inverso es. Debido a que la función dada es una función lineal, se puede representar gráficamente mediante el uso de la forma pendiente-intersección. En primer lugar, el gráfico y = X. La forma pendiente-intersección que da la y-intercepto en (0, -2). Dado que la pendiente es 3 = 3/1, se mueve hacia arriba 3 unidades y más de 1 unidad para llegar en el punto (1, 1). Si usted se muda de nuevo hasta 3 unidades y más de 1 unidad, usted consigue el punto (2, 4). La función inversa, por lo tanto, mueve a través de (-2, 0), (1 1,), y (4, 2). Tanto la función y su inversa se muestran aquí.



Artículos Relacionados

Sobre el autor
Gráficas y funciones de transformación Gráficas y funciones de transformación

Puede graficar funciones bastante cómodamente utilizando una calculadora gráfica, pero se le frustró el uso de esta tecnología, si usted no tiene una buena idea de lo que vas a encontrar y donde usted lo encontrará. Usted necesita tener una…

Cómo calcular un ángulo utilizando funciones trigonométricas inversas Cómo calcular un ángulo utilizando funciones trigonométricas inversas

Casi cada función tiene inversa. Un función inversa básicamente deshace una función. Las funciones trigonométricas seno, coseno y tangente todos tienen inversas, y que a menudo son llamados arcsin, arccos, y arctan.En funciones…

¿Cómo diferenciar funciones inversas ¿Cómo diferenciar funciones inversas

Hay una fórmula difícil buscar la participación de las derivadas de las funciones inversas, pero antes de llegar a eso, a ver la figura siguiente, que resume muy bien la idea.Esta cifra muestra un par de funciones inversas, F y g. Funciones…

Cómo graficar funciones parentales y troncos transformados Cómo graficar funciones parentales y troncos transformados

Quieres un poco de buenas noticias, de forma gratuita? Representación gráfica de funciones de los padres y los registros transformadas es muy fácil! Usted puede cambiar cualquier registro en una expresión exponencial, por lo que este paso es lo…

Cómo invertir una función para encontrar su inversa Cómo invertir una función para encontrar su inversa

Si te dan una función y debe encontrar su inversa, primero recordar que los lugares de dominio y de swap rango en las funciones. Literalmente, intercambias F(X) Y X en la ecuación original. Al realizar ese cambio, se llama a la nueva F(X) Por su…

¿Cómo resolver un sistema de ecuaciones utilizando la inversa de una matriz ¿Cómo resolver un sistema de ecuaciones utilizando la inversa de una matriz

Si usted tiene un coeficiente ligado a una variable en un lado de una ecuación matricial, se puede multiplicar por inversa del coeficiente de hacer ese coeficiente desaparece y te deja con sólo la variable. Por ejemplo, si 3X = 12, ¿cómo…

Cómo para verificar la inversa de una función Cómo para verificar la inversa de una función

A veces, su libro de texto o maestro puede pedirle que verifique que dos funciones dadas son en realidad inversas entre sí. Para ello, es necesario demostrar que tanto F(g(X)) Y g(F(X)) = X.Cuando se le pide que encontrar una inversa de una…

¿Cómo trabajar con líneas en el cálculo ¿Cómo trabajar con líneas en el cálculo

Una línea es la función más simple que se puede representar gráficamente en el plano de coordenadas. (Líneas son importantes en el cálculo porque cuando te acercas lo suficiente en una curva, se ve y se comporta como una línea.) Esta figura…

Funciones Gráfico de seno y coseno inversa Funciones Gráfico de seno y coseno inversa

Las gráficas de las funciones trigonométricas inversas son relativamente singularidad por ejemplo, seno inverso y el coseno inversa son un poco brusca y desarticulada. Estos gráficos son importantes debido a su impacto visual. Especialmente en el…

Funciones Gráfico tangente inversa y cotangente Funciones Gráfico tangente inversa y cotangente

Las gráficas de las funciones tangente y cotangente son muy interesantes porque implican dos asíntotas horizontales. Las asíntotas ayudan con las formas de las curvas y hacer hincapié en el hecho de que algunos ángulos no funcionarán con las…

¿Cómo encontrar una función trigonométrica inversa ¿Cómo encontrar una función trigonométrica inversa

Las funciones trigonométricas inversas todos tienen, pero sólo en condiciones especiales - usted tiene que restringir los valores de dominio. No todas las funciones tienen inversos, y no todos los inversos son fáciles de determinar. Aquí es un…

¿Cómo encontrar la inversa de una función trigonométrica ¿Cómo encontrar la inversa de una función trigonométrica

Utilice las funciones trigonométricas inversas para resolver ecuaciones como pecado X = 1/2, sec X = -2, O moreno 2X = 1. En las ecuaciones típicas de álgebra, puede resolver por el valor de X dividiendo cada lado de la ecuación por el…

» » » » Cómo graficar la inversa de una función