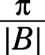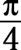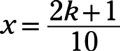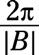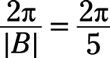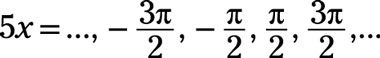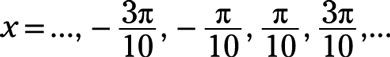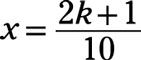Representación gráfica de funciones trigonométricas en pre-cálculo
Las gráficas de funciones trigonométricas son generalmente fácilmente reconocible - después de que se familiarice con el gráfico básico para cada función y las posibilidades de transformaciones de los gráficos básicos.
Funciones trigonométricas son periódica. Es decir, se repiten los mismos valores de la función una y otra, por lo que sus gráficas repetir la misma curva y otra vez. El truco es reconocer la frecuencia de esta curva se repite y donde uno de los gráficos básicos comienza para una función particular.
Una característica interesante de cuatro de las funciones trigonométricas es que tienen asíntotas - esas no-realmente-hay líneas utilizadas como guías para la forma de una curva. Las funciones seno y coseno no tienen asíntotas, porque sus dominios son todos los números reales. Las otras cuatro funciones tienen asíntotas verticales para marcar donde sus dominios tienen lagunas.
Usted va a trabajar con los gráficos de funciones trigonométricas de las siguientes maneras:
Marcado cualquier intercepta en la X-eje para ayudar gráfico de las curvas
Localización y dibujo en asíntotas verticales de la tangente, cotangente, secante y cosecante
Cálculo del cambio en el período de una función basada en alguna transformación
Ajuste de la amplitud de la seno o coseno cuando la curva básica tiene un multiplicador
Haciendo de lado se mueve cuando transformaciones implican traducciones horizontales
Mudanza funciones trigonométricas arriba o hacia abajo con traducciones verticales
Al graficar funciones trigonométricas, algunos desafíos incluirán
No malinterpretar el período de la función trigonométrica cuando una transformación implica una fracción
Dibujo ciclos completos suficientes de la curva para mostrar sus características adecuadamente
Marcar los ejes apropiada para la situación
Haciendo uso de intercepciones cuando son útiles en un gráfico
Problemas de práctica
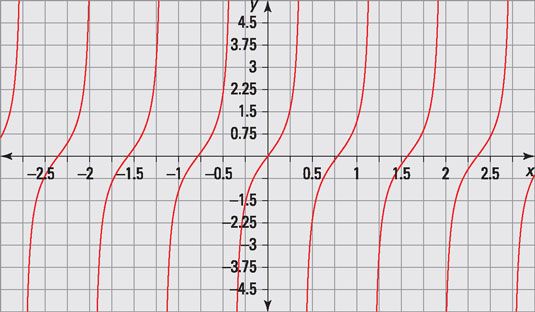
Dibuje la gráfica de la función: F(X) = Tan (4X)
Responder:
La función dada es F(X) = Tan (4X).
Usando F(X) = LAbronceadoBx, el periodo de la función está determinada por
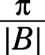
Por lo tanto, la gráfica es la función tangente estándar, excepto con un período de
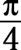
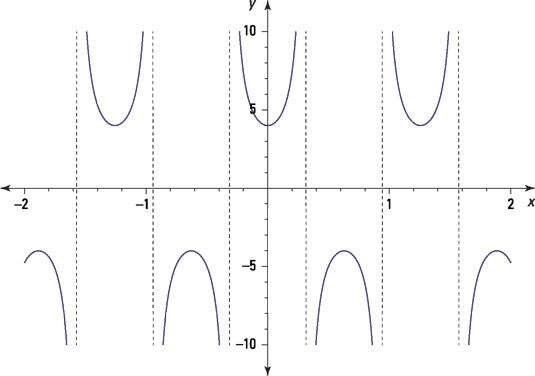
Dar una regla para las ecuaciones de las asíntotas. Luego trace la gráfica de la función: F(X) = 4 segundos (5X)
Responder:
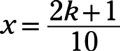
Usar g(X) = LApecadoB(X + C) + D, dónde LA es la amplitud,
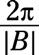
es el período, C representa un desplazamiento horizontal, y D representa un desplazamiento vertical. por F(X) = 4 segundos (5X), El período es
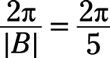
El multiplicador 4 trae las curvas superior hacia abajo a 4 y las curvas inferiores de hasta # 8210-4.
Las asíntotas se encuentran donde el recíproco de la secante, F(X) = 4cos (5X), Es igual a 0: cos5X = 0 cuando
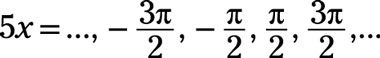
La solución para X, divide cada término por 5 para obtener
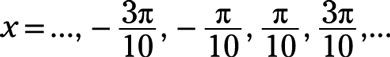
Dejando k sea un número entero, la regla general para las ecuaciones de las asíntotas se
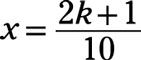
Sobre el autor
 Cómo graficar una función tangente
Cómo graficar una función tangente La función tangente tiene una gráfica de los padres al igual que cualquier otra función. Utilizando la gráfica de esta función, se puede hacer el mismo tipo de transformación que se aplica a la gráfica de los padres de cualquier función. La…
 Cómo graficar seno, coseno y tangente
Cómo graficar seno, coseno y tangente Así, es necesario graficar un seno, coseno, tangente o función. Seno, coseno y tangente - y sus inversos, cosecante, secante y cotangente - son periódico funciones, lo que significa que sus gráficos contienen una forma básica que se repite una…
 Graficar una función seno usando amplitud
Graficar una función seno usando amplitud La función seno y cualquiera de sus variaciones tienen dos características importantes: la amplitud y periodo de la curva. Puede determinar estas características examinado sea la gráfica de la función o su ecuación.los amplitud de la función…
 Funciones Gráfico de seno y coseno inversa
Funciones Gráfico de seno y coseno inversa Las gráficas de las funciones trigonométricas inversas son relativamente singularidad por ejemplo, seno inverso y el coseno inversa son un poco brusca y desarticulada. Estos gráficos son importantes debido a su impacto visual. Especialmente en el…
 Funciones Gráfico tangente inversa y cotangente
Funciones Gráfico tangente inversa y cotangente Las gráficas de las funciones tangente y cotangente son muy interesantes porque implican dos asíntotas horizontales. Las asíntotas ayudan con las formas de las curvas y hacer hincapié en el hecho de que algunos ángulos no funcionarán con las…
 Funciones Gráfico tangentes con multiplicadores variables
Funciones Gráfico tangentes con multiplicadores variables En trigonometría, multiplicando el ángulo variable en una función tangente tiene el mismo efecto como lo hace con funciones seno y coseno - que afecta el periodo de la función. Si el múltiplo es 2, como en y = Tan 2X, a continuación, la…
 Graficar las asíntotas de una función cotangente
Graficar las asíntotas de una función cotangente Las gráficas de la función tangente sientan las bases para las gráficas de la función cotangente. Después de todo, la tangente y cotangente son cofunciones y recíprocos, y tienen todo tipo de conexiones.Las gráficas de estas dos funciones son…
 Grafica la función cosecante
Grafica la función cosecante Una manera muy eficaz de graficar la función cosecante es hacer primero un boceto rápido de la función seno (su recíproco). Con el boceto de seno en su lugar, se puede dibujar las asíntotas de la función cosecante a través de la X-intercepta…
 Grafica la asíntota de una función tangente
Grafica la asíntota de una función tangente Un asíntota es una línea que ayuda a dar sentido a una gráfica de una función trigonometría. Esta línea no es parte del ficos de la función sino que ayuda a determinar la forma de la curva, mostrando donde la curva tiende a ser una línea…
 Variaciones Gráfico en una función secante
Variaciones Gráfico en una función secante La gráfica de una función secante es diferente de la cosecante de varias maneras, pero una de las maneras más evidentes es que la gráfica de la secante es simétrica con respecto al y-eje. El secante es un espejo de reflexión sobre ese eje.…
 Graficar las asíntotas de una función secante
Graficar las asíntotas de una función secante Para graficar la curva de la secante, primero identificar las asíntotas determinando donde el recíproco de la secante - coseno - es igual a 0. Luego de realizar el boceto en ese recíproco, para que pueda determinar los puntos de inflexión y la…
 Cómo reconocer los gráficos básicos trigonométricas
Cómo reconocer los gráficos básicos trigonométricas Las gráficas de las funciones trigonométricas tienen muchas similitudes y muchas diferencias. Los gráficos del seno y el coseno parecen mucho, al igual que la tangente y cotangente, y luego la secante y cosecante tienen similitudes. Pero esos…