Grafica la asíntota de una función tangente

Un asíntota es una línea que ayuda a dar sentido a una gráfica de una función trigonometría. Esta línea no es parte del ficos de la función sino que ayuda a determinar la forma de la curva, mostrando donde la curva tiende a ser una línea recta - en algún lugar. Asíntotas generalmente se indican con líneas de trazos para distinguirlos de la función real.

Las asíntotas de la gráfica de la función tangente son líneas verticales que se producen regularmente, cada una de ellas pi-, o 180 grados, aparte. Se separan cada pieza de la curva tangente, o cada ciclo completo de la siguiente.

Las ecuaciones de las asíntotas de la tangente son todos de la forma

dónde n es un número entero. Bajo esta estipulación para n, la expresión 2n + 1 siempre resulta en un número impar. Mediante la sustitución de n con varios números enteros, se obtiene líneas como

La razón de que asíntotas siempre ocurre en estos múltiplos impares de

es porque esos puntos es donde la función coseno es igual a 0. Como tal, el dominio de la función tangente incluye todos los números reales excepto los números que se producen en estos asíntotas.

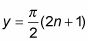
La figura anterior muestra lo que las asíntotas parecen cuando graficada solo.

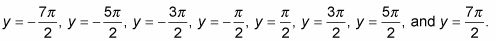
La primera figura no es tan emocionante, pero muestra cómo muchas veces la función tangente reitera su patrón. Ahora echa un vistazo a la segunda cifra anterior, lo que muestra un ciclo de la función tangente en un gráfico. Los valores tangentes van infinitamente alto como la medida del ángulo se aproxima a 90 grados. Los valores van infinitamente bajo como la medida del ángulo se aproxima a -90 grados.

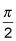
En la tercera figura, hay más de la tangente en un gráfico, asíntotas incluidos, para darle una mejor idea de lo que está pasando.

Como puede ver, la función tangente repite sus valores y otra vez. La principal diferencia entre esta función y las funciones seno y coseno es que la tangente tiene todas estas pausas entre los ciclos. A medida que avanza de izquierda a derecha, la tangente parece ir hasta el infinito positivo. En realidad, desaparece en la parte superior de la gráfica y luego recoge de nuevo en la parte inferior, donde los valores vienen desde el infinito negativo. Las calculadoras gráficas y otras utilidades gráficas por lo general no muestran el gráfico de desaparecer en la parte superior, por lo que le toca a usted para saber lo que está sucediendo realmente, a pesar de que la imagen puede no ser exactamente de esa manera.

Una de las peculiaridades de las calculadoras gráficas es que intentan conectar la función tangente para que sea continua a través de la pantalla. Por esta razón, se le suele ver algunas líneas entre las diferentes partes de la curva. En cierto modo, estas líneas son errores - no son las asíntotas, si bien usted puede estar tentado a pensar que son. La única manera de deshacerse de esas líneas adicionales es dar vuelta a la calculadora para el modo de punto (en comparación con el modo conectado). La mayoría de las calculadoras tienen formas de configurar los ajustes (o modo) para cosas tales como grados y radianes, gráficos de puntos y gráficos conectados, decimales flotantes y decimales fijos, y así sucesivamente. Los cambios son generalmente fáciles de hacer - simplemente consulte el manual de la calculadora para obtener instrucciones específicas. La parte difícil es recordar lo que el establecimiento que se encuentre.