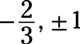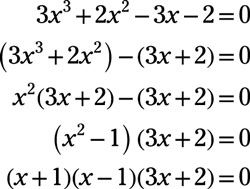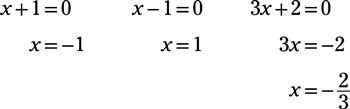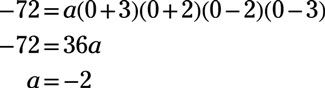Polinomios y pre-cálculo
Funciones polinómicas tienen gráficos que son curvas suaves. Ellos van de menos infinito a más infinito en un agradable, que fluye de la moda, sin cambios bruscos de dirección. Piezas de funciones polinómicas son útiles al modelar situaciones físicas, tales como la altura de un disparo de cohetes en el aire o el tiempo que una persona necesita para nadar una vuelta en función de su edad.
La mayor parte de la atención en funciones polinómicas es en la determinación de cuando la función cambia de valores negativos a valores positivos o viceversa. También es de interés cuando la curva llega a un punto relativamente alto o relativamente bajo punto. Algunas buenas técnicas de álgebra recorrer un largo camino hacia el estudio de estas características de las funciones polinómicas.
Usted trabajará con funciones polinómicas de las siguientes maneras:
Resolución de ecuaciones cuadráticas por factorización o usando la fórmula cuadrática
Reescribiendo ecuaciones cuadráticas completando el cuadrado
Factoring polinomios utilizando agrupación
Buscando las raíces racionales de polinomios utilizando el teorema de la raíz racional
Contando raíces reales con la regla de los signos de Descartes
El uso de división sintética para calcular rápidamente factores
Escribiendo ecuaciones de polinomios dado raíces y otra información
Representación gráfica de polinomios utilizando-comportamiento extremo y la forma factorizada
No deje viaje de errores comunes que UP- tener en cuenta que cuando se trabaja con funciones polinómicas, sus retos incluirán
Observando el orden de las operaciones cuando se utiliza la fórmula cuadrática
Agregando a ambos lados al completar el cuadrado
Recordando a insertar ceros para los términos que faltan cuando se utiliza la división sintética
Reconociendo el efecto de las raíces imaginarias en la gráfica de un polinomio
Problemas de práctica
Encuentra las raíces reales (X-intercepta) del polinomio utilizando la factorización agrupando.
3X3 + 2X2 - 3X - 2 = 0
Responder:
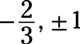
En primer lugar, factor por el agrupamiento. Romper el polinomio en conjuntos de dos y luego encontrar el máximo común divisor de cada set y el factor a cabo. Finalmente, el factor de nuevo.
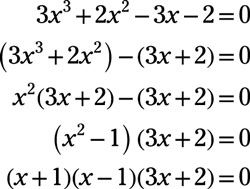
A continuación, establezca cada factor igual a cero y resolver para X para encontrar la X-intercepta:
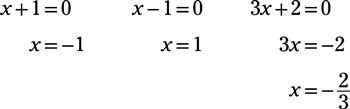
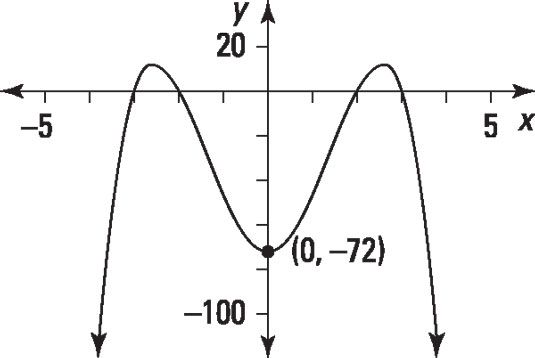
Escribe una ecuación para la gráfica polinomio dado.
Responder: F(X) = -2X4 + 26X2 - 72
La gráfica cruza el X-eje a x = -3, x = -2, x = 2, y x = 3, por lo que la función está dada por
F(X) = la(X + 3) (X +2) (X -2) (X -3)
dónde la es una constante. los y-intersección es (0, -72), por lo que encontrar la mediante la conexión de estos valores y resolución:
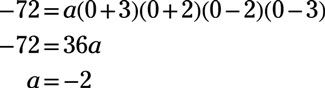
Por lo tanto, la función es F(X) = -2 (X +3) (X + 2) (X -2) (X - 3) = -2X4 + 26X2 -72
-
Herramientas de álgebra en el menú de la aplicación calculadora TI-Nspire -
1,001 Álgebra practico problemas para los maniquíes - 1.001 Álgebra problemas de práctica ii para los maniquíes
- Álgebra II: oculto intersecciones de las curvas
-
Desenterrar raíces polinómicas con factoring - Funciones polinómicas y ecuaciones de álgebra ii
Los fundamentos de la resolución de ecuaciones de álgebra i Uno de los objetivos más comunes en álgebra I es resolver una ecuación. Resolver una ecuación significa para identificar el número o números que puede reemplazar la variable con hacer una declaración verdadera. Usted encontrará el factoring…
Conceptos básicos de cómo adivinar y comprobar raíces reales Puede utilizar el teorema de la raíz racional para restringir la búsqueda de las raíces de los polinomios. Si bien la regla de los signos de Descartes sólo se estrecha hacia abajo las raíces reales en positivo y negativo, el teorema de la raíz…
Las funciones exponenciales y logarítmicas utilizados en pre-cálculo Las funciones exponenciales y logarítmicas van de la mano. Usted no pensaría así, a primera vista, porque las funciones exponenciales pueden parecer F(X) = 2e3X, y logarítmicas (log) pueden parecer F(X) = Ln (X2 - 3). Lo que los une es que las…
Expresar y se aproximan a las funciones utilizando la serie de Taylor Es importante entender la diferencia entre eXpressing una función como una serie infinita y lapproximating una función mediante el uso de un número finito de términos de la serie. Usted puede pensar en una serie de potencias como un polinomio…
Encontrar las raíces de una ecuación factorizada En pre-cálculo, puede utilizar la propiedad del producto cero a encontrar las raíces de una ecuación factorizada. Después se toma un polinomio en sus diferentes piezas, puede configurar cada pieza igual a cero para resolver las raíces con la…
Gráficas y funciones de transformación Puede graficar funciones bastante cómodamente utilizando una calculadora gráfica, pero se le frustró el uso de esta tecnología, si usted no tiene una buena idea de lo que vas a encontrar y donde usted lo encontrará. Usted necesita tener una…
Cómo calcular salidas para funciones racionales En pre-cálculo, se puede calcular salidas para funciones racionales. LA función racional es una función que se puede expresar como el cociente de dos polinomios, de tal manera quedonde el grado de q(X) Es mayor que cero.Estos son los pasos a…
¿Cómo encontrar raíces imaginarias usando el teorema fundamental del álgebra El teorema fundamental del álgebra puede ayudarle a encontrar las raíces imaginarias. Raíces imaginarias aparecerá en una ecuación de segundo grado cuando el discriminante de la ecuación de segundo grado - la parte bajo el signo de la raíz…
¿Cómo encontrar las raíces reales de un polinomio utilizando la regla de los signos de Descartes Si sabe el número de raíces totales un polinomio tiene, puede utilizar un teorema muy bien llamada Regla de los signos de Descartes a contar cuántas raíces son números reales (tanto positivos y negativa) y cuántos son imaginarios. Usted ve, el…
Cómo graficar polinomios Aunque puede parecer desalentador, graficar polinomios es un proceso bastante sencillo. Una vez que haya encontrado los ceros de un polinomio, puede seguir unos sencillos pasos para representarla gráficamente.Por ejemplo, si ha encontrado los ceros…
Cómo graficar polinomios cuando las raíces son números imaginarios - una visión general En pre-cálculo y en el cálculo, ciertas funciones polinómicas tener raíces no reales además de raíces reales (y algunas de las funciones más complicadas tener todas raíces imaginarias). Cuando usted debe encontrar tanto, empezar por la…
¿Cómo adivinar y comprobar raíces reales - 2 - raíces de pruebas por polinomios en división usando la división larga Una vez que haya utilizado el teorema de la raíz racional para enumerar todos los posibles raíces racionales de cualquier polinomio, el siguiente paso es poner a prueba las raíces. Una forma es utilizar la división larga de polinomios y la…