Evaluando el área de un polígono

No sólo pueden polígonos pueden clasificar por el número de lados que tienen y por sus ángulos, pero también pueden ser agrupados de acuerdo a algunas de sus cualidades. Los polígonos pueden tener tres características de la personalidad: equiláteros, equiangulares y regulares.

En una equilátero polígono, todos los lados son iguales y hay al menos un ángulo nonsimilar. En una equiángulo polígono, todos los ángulos son iguales y al menos un lado no coincide con la longitud de los otros. LA regular polígono es tanto equilátero y equiangular- tiene total simetría - lados iguales y ángulos iguales.

Algunas líneas son especiales

Cuando se dispuso a encontrar el área de un polígono regular, hay que tener en cuenta que los polígonos regulares tienen líneas con un significado especial. Estas líneas incluyen el radio y la apotema.

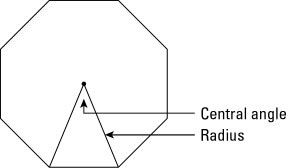
los radio es una línea que va desde el centro del polígono en un codo (o vértice si prefiere el balbuceo técnica) del polígono - dividir ese ángulo uniformemente en dos. Cuando dos radios diferentes en un polígono son atraídos a dos vértices consecutivos, se forma un ángulo central en el centro del polígono (véase la Figura 1).

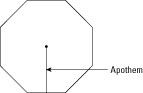
A diferencia de la radio, que corta un ángulo, una apotema se extiende desde el centro del polígono directamente a un lado plano del polígono. En el impacto, la apotema se convierte en una mediatriz del lado choca con (véase la Figura 2).

Una fiesta de teoremas

Una serie de teoremas existe para radios, ángulos centrales y apothems de polígonos regulares. He aquí un resumen para su placer de la lectura:

• Teorema 5.8: Radios de un polígono regular bisecan el ángulo interior.
• Teorema 5.9: Ángulos centrales de un polígono regular son congruentes.
• Teorema 5-10: Ángulos centrales de polígonos regulares con los lados iguales son congruentes.
• Teorema 5.11: La medida de un ángulo central de un polígono regular es igual a 360 # 176- dividido por el número de lados del polígono.
• Teorema 12.5: Un apotema de un polígono regular biseca el ángulo central (determinado por el lado) a la que se dibuja.
• Teorema 5.13: Un apotema de un polígono regular es una bisectriz perpendicular al lado se señala a.

Poniendo todo junto

Usted puede calcular el área de un polígono regular utilizando la longitud de su apotema y la longitud de su perímetro: Es necesario inspeccionar el perímetro y determinar su longitud. Usar la información acerca de la longitud de un lado. Debido a que el polígono es regular, las longitudes son las mismas para cada lado. Multiplique el número de lados del polígono por la longitud de un lado, y se obtiene el perímetro. El área de un polígono regular es igual a la mitad del producto de la apotema y el perímetro.

Teorema 5-14: La fórmula para el área de un polígono regular es LA = 1/2ap, dónde la es la apotema y p es el perímetro.

Traducción: Si usted tiene un polígono regular, conecte la longitud de la apotema y el perímetro en la fórmula, y se obtiene la zona.

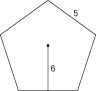
Echa un vistazo a la figura 3 para un ejemplo. La información proporcionada indica que la longitud de un lado del pentágono es igual a 5 y que la apotema es igual a 6. Antes de poder determinar el área, primero debe calcular el perímetro. Si la longitud de un lado de un pentágono es 5, entonces el perímetro es igual a una longitud lateral de 5 multiplicado por cinco lados. Así que el perímetro total del pentágono es igual a 25. Si conecta esta información en la fórmula del área, se obtiene lo siguiente:

LA = 1/2 (6) (25)

A = 1/2 (150)

LA = 75

Por lo tanto el área del pentágono en la figura 3, con la información dada, es de 75 unidades cuadradas.

Ahora considere esto: Así como usted puede añadir segmentos de líneas y ángulos, también puede añadir áreas.

Postulado 1.5: Si un polígono encierra regiones más pequeñas, que no se solapan dentro de su perímetro, entonces el área de ese polígono es igual a la suma de las áreas de las regiones cerrados.

Echa un vistazo a el polígono cóncavo en la figura 4. Para encontrar el área total de la figura, obtener el área de las secciones que se pueden obtener fácilmente. Mira de cerca: En realidad se puede romper el polígono en dos rectángulos que no se superponen. Encuentra el área de cada rectángulo y luego sumarlos. A continuación, tiene la zona de todo el polígono.