¿Cómo encontrar el número de diagonales de un polígono
Para encontrar el número de diagonales de un polígono con n lados, use la siguiente fórmula:
Esta fórmula parece que venía Vete de la nada, ¿no? Por supuesto, no hay fórmulas matemáticas salido de la nada, pero es posible que tenga que pensar en éste un poco para descubrir la lógica detrás de él. (Sólo memorizando que está bien, pero ¿qué hay de divertido en eso?)
Aquí es donde la fórmula diagonal viene y por qué funciona. Cada diagonal conecta un punto a otro punto en el polígono que no es su vecino de al lado. En una n-polígono cara, usted tiene n puntos de partida para diagonales. Y cada diagonal puede ir a (n - 3) que termina puntos porque una diagonal no puede terminar en su propio punto de partida o en cualquiera de los dos puntos vecinos. Así que el primer paso es multiplicar n por (n - 3). Entonces, debido a punto final de cada diagonal se puede utilizar como punto de partida, así, el producto n(n - 3) que cuenta cada diagonal dos veces. Es por eso que se divide por 2.
Esto es un problema para usted: si un polígono tiene 90 diagonales, ¿cuántos lados tiene?
¿Sabes lo que la fórmula para el número de diagonales de un polígono es, y usted sabe que el polígono tiene 90 diagonales, por lo enchufa 90 en la respuesta y resolver para n:
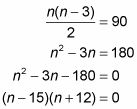
Por lo tanto, n es igual a 15 o -12. Pero debido a un polígono no puede tener un número negativo de lados, n debe ser 15. Por lo que tiene un polígono de 15 lados (un pentadecágono, en caso de que usted es curioso).
Esto es una aplicación en el mundo real ingenioso de la fórmula diagonal. Digamos que hay un pequeño torneo de tenis con seis personas en la que todo el mundo tiene que jugar todos los demás. ¿Cuántos partidos totales habrá? La siguiente figura muestra los seis jugadores de tenis con segmentos que conectan cada par de jugadores.
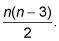
Cada segmento representa un partido entre dos concursantes. Así que para obtener el número total de partidos, sólo hay que contar hasta todos los segmentos de la figura: el número de lados del hexágono (6) más el número de diagonales en el hexágono
Por tanto, el total es de 15 partidos. Para el caso general, el número total de partidos en un torneo round-robin con n jugadores serían
Juego, set, partido.
Construir polígonos regulares con TI-84 Plus GeoMaster Un polígono regular se determina por su centro y el número de sus lados. Puede utilizar el GeoMaster DIBUJAR menú de la TI-84 Plus calculadora gráfica para crear polígonos regulares e irregulares, círculos, triángulos, y muchas otras formas…
Encuentre el área de un polígono que tiene lados que se cruzan GeoMaster en el Plus calculadora TI-84 puede ayudar a encontrar el área de un polígono que tiene lados que se cruzan. Para encontrar el área de un polígono que tiene lados que se cruzan, romper el polígono hacia abajo en polígonos simples…
Encuentra el área con GeoMaster en la TI-84 Plus GeoMaster en la TI-84 Plus calculadora gráfica puede encontrar el área de cualquier círculo, triángulo, o sencillo polígono construido usando el Círculo, Triángulo, Polígono, o RegPolygon herramienta en el DIBUJAR menú. Un polígono es…
Cómo usar el menú de la transformación de TI-Nspire El menú Transformación ofrece cinco transformaciones diferentes: Simetría, reflexión, traslación, rotación y dilatación. He aquí una breve descripción de lo que cuatro de las herramientas de transformación se puede hacer y lo que haces…
Problemas de la práctica de la geometría con triángulos y polígonos LA polígono es una figura geométrica que tiene al menos tres lados. El triángulo es el polígono más básico. Usted encontrará las siguientes fórmulas y propiedades útiles al responder a las preguntas que implican desigualdades triángulo,…
Fórmulas de geometría que usted debe saber A continuación se presentan algunas de las fórmulas de geometría más importantes, teoremas, propiedades, etc. que se utilizan para resolver diversos problemas. Si te quedas perplejo mientras se trabaja en un problema y no puede llegar a una…
Cómo calcular el área de un hexágono regular Una forma de encontrar el área de un hexágono regular es de primera división en triángulos equiláteros. También es necesario utilizar un apotema - un segmento que une el centro de un polígono regular hasta el punto medio de cualquier lado y…
Cómo calcular el área de un polígono regular LA polígono regular es equilátero (tiene lados iguales) y equiangular (tiene ángulos iguales). Para encontrar el área de un polígono regular, se utiliza un apotema - un segmento que une el centro del polígono al punto medio de cualquier lado y…
Cómo calcular el área de un cometa Usted calcula el área de un cometa mediante el uso de las longitudes de sus diagonales. He aquí un ejemplo: ¿cuál es el área de la cometa COMETA en la siguiente figura?Para los problemas de la cometa zona (y algunas veces otros problemas…
¿Cómo encontrar el área de la intersección de dos polígonos GeoMaster en la calculadora gráfica TI-84 no puede encontrar el área de un polígono formado por la intersección de otros dos polígonos porque GeoMaster no sabe que está ahí. Para obtener GeoMaster para encontrar el área de la intersección,…
Interior y ángulos exteriores de un polígono Todo lo que necesita saber acerca de un polígono no necesariamente comprendido en sus lados. Usted puede necesitar para encontrar ángulos exteriores, así como ángulos interiores cuando se trabaja con polígonos:Ángulo interior: Un ángulo…
Evaluando el área de un polígono No sólo pueden polígonos pueden clasificar por el número de lados que tienen y por sus ángulos, pero también pueden ser agrupados de acuerdo a algunas de sus cualidades. Los polígonos pueden tener tres características de la personalidad:…