Cómo usar el menú de la transformación de TI-Nspire

El menú Transformación ofrece cinco transformaciones diferentes: Simetría, reflexión, traslación, rotación y dilatación. He aquí una breve descripción de lo que cuatro de las herramientas de transformación se puede hacer y lo que haces para llevar a cabo la transformación:

• Simetría: Esta transformación da la imagen de un objeto con una rotación de 180 grados alrededor de un punto.

• Reflexión: Esta transformación da la imagen de un objeto se refleja sobre una línea o segmento.

• Traducción: Esta transformación da la imagen de un objeto traducido por una distancia y dirección dada por un vector o dos puntos.

• Dilatación: Esta transformación da la imagen de un objeto con un punto que es el centro de dilatación y un número que especifica el factor de dilatación.

La primeras dos transformaciones, la simetría y la reflexión, se lleva a cabo utilizando pasos similares. Estos son los pasos para reflejar un polígono sobre una línea:

1. Dibuja un polígono.

2. Dibuja un segmento o línea.

3. Pulse [MENU] -Transformación-Reflexión para abrir la herramienta de reflexión.

4. Haga clic en el polígono.

5. Haga clic en el segmento o línea.

   Cuando se utiliza la herramienta Simetría, haga clic en un punto.

6. Presione [ESC] para salir de la herramienta Reflejo.

Estos son los pasos para usar la herramienta de traducción:

1. Dibuje un objeto.

2. Dibuje un vector (o dos puntos) que da la dirección y longitud de la traducción.

3. Pulse [MENU] -Transformación-traducción para abrir la herramienta de traducción.

4. Haga clic en el objeto.

5. Haga clic en el vector (o cada uno de los dos puntos).

6. Presione [ESC] para salir de la herramienta de traducción.

La primera pantalla muestra los resultados del uso de las herramientas de la simetría, la reflexión y de traducción. Comience por dibujar polígonos LA. A continuación, utilice la herramienta Simetría para completar una rotación de 180 grados del polígono LA alrededor del punto p, que produce polígono B.

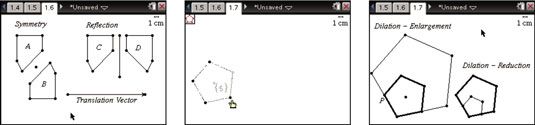
La herramienta de traducción se utiliza para traducir polígono LA al polígono C. Para completar este paso, haga clic en polígono LA y luego el vector de traslación situado en la parte inferior de la pantalla (para dibujar un vector, pulse [MENU]-Puntos Líneas-vector). Tenga en cuenta que los puntos correspondientes en los polígonos LA y C están situados a una distancia y dirección igual a la del vector de traducción.

Por último, utilice la herramienta de reflexión para completar el reflejo del polígono C sobre la línea. Intente arrastrar objetos y observar los cambios correspondientes.

Para realizar una dilatación, siga estos pasos:

1. Dibuja un pentágono regular con la herramienta Polígono regular. Pulse [MENU] Polígono -Shapes-Regular para abrir la herramienta.

2. Mueva el cursor a un punto existente o cualquier espacio abierto en la página y pulse [CLICK] para marcar el punto de partida.

3. Utilice el panel táctil para mover el cursor de distancia del centro del polígono regular y pulse [CLICK] para establecer el radio y el primer vértice del polígono regular.

4. Utilice el panel táctil para mover el cursor hacia la derecha. Esta acción disminuye el número de lados del polígono regular. Pulse [ENTER] cuando el número de lados es 5.

   Tome un minuto para jugar con esta herramienta. Usted puede tener un máximo de 16 lados, y usted puede crear estrellas y otras formas cuando se mueve a menos de tres lados.

   En el aula, puede utilizar la herramienta Polígono regular como una buena visual para demostrar de forma dinámica que las más caras que usted tiene, cuanto más cerca del área del polígono llega al área de un círculo con el mismo radio.

5. Pulse [MENU] -Transformación-dilatación para abrir la herramienta de dilatación.

6. Haga clic en el punto que define el centro de la dilatación.

7. Escriba un número para dar la escala o dilatación factor continuación, pulse [ENTER].

8. Haga clic en el objeto, que en este caso es el pentágono.

9. Presione [ESC] para salir de la herramienta de dilatación.

La tercera pantalla muestra el resultado de usar la herramienta de dilatación. A la izquierda hay una dilatación que se traduce en una ampliación con un factor de escala de 2 y el centro de la dilatación en el punto P. La imagen se muestra con líneas de peso medio, y de la imagen inversa se muestra con líneas de peso delgada.

A la derecha es una dilatación que se traduce en una reducción con un factor de escala de 2/3.