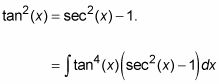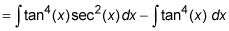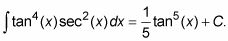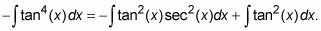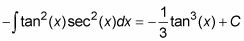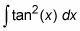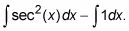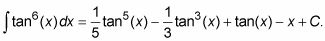¿Cómo integrar los problemas con un par, el poder positivo de la tangente
He aquí cómo usted integra un integrante trig que contiene tangentes (y no hay factores secantes) donde el poder tangente es uniforme y positiva.
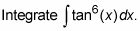
Convertir un bronceado cuadrado (X) Factor a secantes mediante el uso de la identidad de Pitágoras.
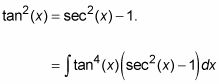
Distribuir y dividir la integral.
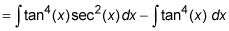
Resuelve la primera integral de sustitución utilizando, cuando u = Tan (X) Y du = sec2(x) dx.
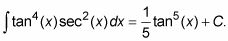
Para la segunda integral, repita el proceso que se muestra en los pasos 1 y 2 anteriores.
Para esta parte del problema, se obtiene
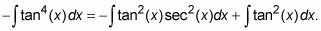
Por primera integrante de inmediato anterior, repita el paso 3.
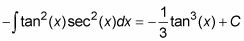
Para el segundo integrante de la Etapa 4, use la identidad de Pitágoras para convertir el
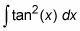
dentro
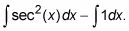
Ambos de estas integrales se puede hacer con las reglas de diferenciación inversas simples.
Después de recoger todas estas piezas - pieza 1 de la Etapa 3, la pieza 2 de la Etapa 5, y las piezas 3 y 4 de Paso 6 - su respuesta final debe ser
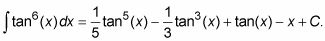
Pedazo de pastel.
-
Cómo evaluar una integral impropia que es horizontalmente infinita -
Cómo evaluar una integral impropia que es verticalmente infinita -
¿Cómo integrar potencias pares de secantes con tangentes -
¿Cómo integrar mediante el uso de fracciones parciales cuando el denominador contiene sólo factores lineales -
¿Cómo integrar potencias impares de tangentes con secantes -
¿Cómo integrar los problemas de seno / coseno con una potencia extraña, positivo de seno
¿Cómo integrar tangentes / problemas secantes con un par, el poder positivo de la secante He aquí cómo usted integra un integrante trig que contiene tangentes y secantes donde el poder secante es par y positiva. Al igual que con todas las tangentes / integrales secantes, se utiliza la versión tangente secante de la identidad de…
¿Cómo integrar los problemas de seno / coseno con una potencia extraña, positivo de coseno Mediante la integración de un integrante trig que incluye coseno, y si el poder del coseno es impar y positivo, puede convertir y luego utilizar la sustitución de integrar. Para hacer esta conversión, lo que necesita saber la identidad de…
¿Cómo integrar tangentes / problemas secantes con una potencia extraña, positivo de la tangente He aquí cómo usted integra un integrante trig que contiene tangentes y secantes donde el poder tangente es impar y positivo. Usted necesitará la versión tangente secante de la identidad de Pitágoras:Lop fuera un factor secante-tangente y…
¿Cómo resolver integrales con la sustitución de variables En cálculo, puede utilizar la sustitución de variables para evaluar una integral compleja. Sustitución de variables permite integrar cuando la regla de la suma, la Regla múltiplo constante, y la Regla de energía no funcionan.Declare una…
¿Cómo resolver integrales impropias de funciones que tienen asíntotas verticales A resolver integrales impropias, al convertirlos en problemas de límite. No se puede hacer de ellos la manera regular. He aquí cómo resolver integrales impropias de funciones que tienen asíntotas verticales. Hay dos casos: una asíntota vertical…
Cómo utilizar la sustitución trigonométrica para integrar los radicales de la forma sinusoidal Antes de leer este artículo, usted debe comprobar fuera de la discusión de la sustitución trigonométrica en el artículo complementario, " Cómo utilizar Trig Sustitución de integrar ".Con el método de sustitución trigonométrica, puede…
Integrar, cuando los poderes de seno, coseno son aún, no negativo Cuando los poderes tanto de seno y coseno son uniformes y no negativo, se puede convertir el integrando en potencias impares de cosenos mediante el uso de las siguientes identidades trigonométricas.Dos identidades trigonométricas prácticos:Luego…
Integrar una función utilizando el caso tangente Cuando la función está integrando incluye un término de la forma (la2 + X2)n, llamar su trigonometría triángulo de sustitución para el caso tangente. Por ejemplo, supongamos que desea evaluar la siguiente integral:Este es un caso tangente,…
La integración usando fracciones parciales cuando el denominador contiene factores irreducibles cuadráticas Usted puede utilizar el método de fracciones parciales para integrar las funciones racionales, incluyendo funciones con denominadores que contienen irreducible factores de segundo grado (es decir, los factores de segundo grado que no puede…
Integrar las funciones donde el denominador contiene factores cuadráticos irreducibles A veces no se puede factorizar un denominador todo el camino a factores lineales porque algunas ecuaciones cuadráticas son irreductibles - al igual que los números primos, no pueden tenerse en cuenta.Comprobar el discriminante. Puede comprobar…
La creación de fracciones parciales cuando se ha repetido factores cuadráticos Su primer paso en cualquier problema que involucra fracciones parciales es reconocer cuyo caso usted está tratando con lo que pueda solucionar el problema. Uno de los casos donde se puede utilizar fracciones parciales es con factores cuadráticos…
La creación de fracciones parciales cuando tiene distintos factores Su primer paso en cualquier problema que involucra fracciones parciales es reconocer cuyo caso usted está tratando con lo que pueda solucionar el problema. Uno de los casos donde se puede utilizar fracciones parciales es cuando el denominador es el…