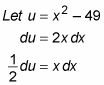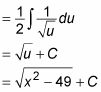Saber cuando para evitar la sustitución de la trigonometría
Es útil saber cuándo debe evitar el uso de la sustitución trigonométrica. Con algunas integrales, es mejor ampliar el problema en un polinomio. Por ejemplo, mira la siguiente integral:
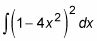
Esto puede parecer un buen lugar para utilizar la sustitución trigonométrica, pero es un lugar aún mejor usar un poco de álgebra para expandir el problema en un polinomio:
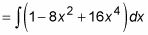
Del mismo modo, mira esta integral:
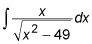
Puede utilizar la sustitución trigonométrica para evaluar esta integral si quieres. (También puede caminar hasta la cima del Empire State Building en lugar de tomar el ascensor si eso hace cosquillas a su fantasía.) Sin embargo, la presencia de ese pequeño X en el numerador debe inclinar que fuera que la sustitución de variables funcionará igual de bien:
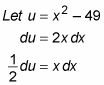
El uso de esta sustitución da como resultado la siguiente integral:
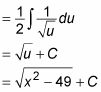
¡Hecho!
-
Cálculo: técnicas de integración -
Encuentra la integral de funciones anidadas -
Cómo evaluar una integral impropia que es verticalmente infinita -
¿Cómo integrar potencias pares de secantes con tangentes -
¿Cómo integrar potencias impares de tangentes con secantes -
¿Cómo integrar potencias impares de senos y cosenos
¿Cómo integrar los problemas de seno / coseno con una potencia extraña, positivo de seno He aquí cómo usted integra un integrante trig que contiene senos y cosenos, donde el poder de seno es impar y positivo. Usted cortar un factor sine y ponerlo a la derecha del resto de la expresión, convertir los restantes (incluso) factores seno…
¿Cómo resolver integrales con la sustitución de variables En cálculo, puede utilizar la sustitución de variables para evaluar una integral compleja. Sustitución de variables permite integrar cuando la regla de la suma, la Regla múltiplo constante, y la Regla de energía no funcionan.Declare una…
¿Cómo resolver límites con álgebra básica Cuando la sustitución no funciona en la función de límite inicial - por lo general a causa de un agujero en la función - a menudo se puede usar un poco de álgebra para manipular la función hasta la sustitución funciona (funciona porque su…
Cómo utilizar l'h & # regla del 244-pital para resolver problemas de límite Regla de L'H # de 244-pital es un gran atajo para hacer algunos problemas de límite. (Y es posible que se necesite algún día para resolver algunos problemas integrales impropias, y también para algunos problemas de series infinitas.)Al igual que…
Cómo utilizar la sustitución de seno para integrar Con el método de sustitución trigonométrica, puede hacerlo integrales que contienen radicales de ciertas formas, ya que coinciden con las funciones trigonométricas. Un seno puede tomar el lugar de un resto en una forma particular.Dibuja un…
Cómo utilizar la sustitución tangente a integrar Con el método de sustitución trigonométrica, puede hacerlo integrales contienen radicales de las siguientes formas:dónde la es una constante y u es una expresión que contiene X.Usted va a encantar esta técnica # 133- tanto como pegar un hierro…
Cómo utilizar la sustitución trigonométrica para integrar Con el método de sustitución trigonométrica, puede hacerlo integrales que contienen radicales de las siguientes formas (dada la es una constante y u es una expresión que contiene X):Usted va a encantar esta técnica ... casi tanto como pegar un…
Cómo utilizar la sustitución trigonométrica para integrar los radicales de la forma sinusoidal Antes de leer este artículo, usted debe comprobar fuera de la discusión de la sustitución trigonométrica en el artículo complementario, " Cómo utilizar Trig Sustitución de integrar ".Con el método de sustitución trigonométrica, puede…
Integrar una función utilizando el caso secante Cuando la función que se está integrando incluye un término de la forma (bx2 - la2)n, llamar su triángulo sustitución trigonométrica para el caso secante. Por ejemplo, suponga que desea evaluar esta integral:Este es un caso secante, debido a…
Integrar una función utilizando el caso sine Cuando la función está integrando incluye un término de la forma (la2 - bx2)n, llamar su triángulo sustitución trigonométrica para el caso sinusoidal. Por ejemplo, supongamos que desea evaluar la siguiente integral:Este es un caso sinusoidal,…
Integrar una función utilizando el caso tangente Cuando la función está integrando incluye un término de la forma (la2 + X2)n, llamar su trigonometría triángulo de sustitución para el caso tangente. Por ejemplo, supongamos que desea evaluar la siguiente integral:Este es un caso tangente,…
La creación de fracciones parciales cuando se ha repetido factores cuadráticos Su primer paso en cualquier problema que involucra fracciones parciales es reconocer cuyo caso usted está tratando con lo que pueda solucionar el problema. Uno de los casos donde se puede utilizar fracciones parciales es con factores cuadráticos…