Cómo utilizar la sustitución trigonométrica para integrar
Con el método de sustitución trigonométrica, puede hacerlo integrales que contienen radicales de las siguientes formas (dada la es una constante y u es una expresión que contiene X):
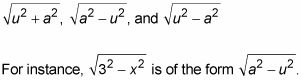
Usted va a encantar esta técnica ... casi tanto como pegar un hierro caliente en el ojo.
Antes de ver las obras de sustitución de la forma trigonométricas, aquí hay algunos trucos mnemotécnicos para ayudarle a mantener este método lineal. Recuerde que con recursos mnemotécnicos, obras tontos (y vulgares). En primer lugar, se trata de tres funciones trigonométricas, tangente, seno, y secante. Sus letras iniciales, t, s, y s, son las mismas letras que las letras iniciales del nombre de esta técnica, trigonometric substitution. Bastante bien, ¿eh?
Bueno, esto mnemotécnica pecado / culo es ciertamente bastante débil. Si se puede llegar a una mejor mnemotécnico, usarlo!
Ahora, listo para hacer un problema?
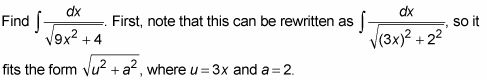
Dibuja un triángulo básicamente justo un SOHCAHTOA triángulo donde
la SOHCAHTOA triángulo se muestra en la siguiente figura.
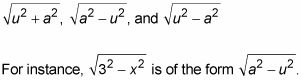
Resolver
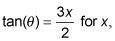
entonces diferenciar y resolver dx.
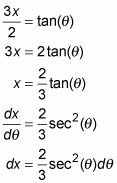
Encuentra función trigonométrica que está representado por el radical sobre el la
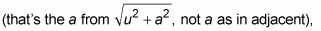
y luego resolver el radical.
Mira el triángulo en la figura. El radical es la hipotenusa y la es 2, la adyacente lado, de modo
Utilizar los resultados de los pasos 2 y 3 para hacer sustituciones en el problema original y luego integrar.
Sustituya la X expresiones de los pasos 1 y 3 de vuelta en de
También puede obtener las expresiones del triángulo en la figura anterior.
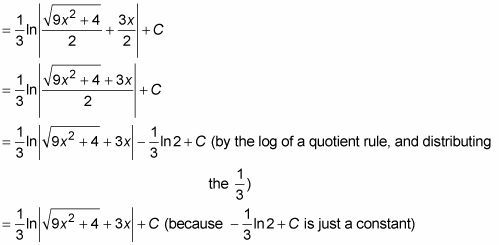
¿Fue divertido o qué?
-
Matemáticas normas fundamentales comunes: similitud, triángulos rectángulos, y trigonometría -
Incluso identidades y pico en las funciones trigonométricas -
Cómo calcular un ángulo utilizando funciones trigonométricas inversas -
Cómo calcular los valores para las seis funciones trigonométricas -
¿Cómo combinar los ángulos de referencia con otras técnicas para resolver ecuaciones trigonométricas -
¿Cómo diferenciar las funciones trigonométricas
¿Cómo resolver integrales con la sustitución de variables En cálculo, puede utilizar la sustitución de variables para evaluar una integral compleja. Sustitución de variables permite integrar cuando la regla de la suma, la Regla múltiplo constante, y la Regla de energía no funcionan.Declare una…
Cómo utilizar la sustitución de seno para integrar Con el método de sustitución trigonométrica, puede hacerlo integrales que contienen radicales de ciertas formas, ya que coinciden con las funciones trigonométricas. Un seno puede tomar el lugar de un resto en una forma particular.Dibuja un…
Cómo utilizar SOHCAHTOA para encontrar las funciones trigonométricas de un triángulo rectángulo El estudio de la trigonometría comienza con el triángulo rectángulo. Las tres funciones principales trigonométricas (seno, coseno y tangente) y sus inversos (cosecante, secante y cotangente) todo lo que dicen algo acerca de las longitudes de los…
Cómo utilizar la sustitución tangente a integrar Con el método de sustitución trigonométrica, puede hacerlo integrales contienen radicales de las siguientes formas:dónde la es una constante y u es una expresión que contiene X.Usted va a encantar esta técnica # 133- tanto como pegar un hierro…
Cómo utilizar la sustitución trigonométrica para integrar los radicales de la forma sinusoidal Antes de leer este artículo, usted debe comprobar fuera de la discusión de la sustitución trigonométrica en el artículo complementario, " Cómo utilizar Trig Sustitución de integrar ".Con el método de sustitución trigonométrica, puede…
Integrar una función utilizando el caso secante Cuando la función que se está integrando incluye un término de la forma (bx2 - la2)n, llamar su triángulo sustitución trigonométrica para el caso secante. Por ejemplo, suponga que desea evaluar esta integral:Este es un caso secante, debido a…
Integrar una función utilizando el caso sine Cuando la función está integrando incluye un término de la forma (la2 - bx2)n, llamar su triángulo sustitución trigonométrica para el caso sinusoidal. Por ejemplo, supongamos que desea evaluar la siguiente integral:Este es un caso sinusoidal,…
Integrar una función utilizando el caso tangente Cuando la función está integrando incluye un término de la forma (la2 + X2)n, llamar su trigonometría triángulo de sustitución para el caso tangente. Por ejemplo, supongamos que desea evaluar la siguiente integral:Este es un caso tangente,…
Trabajar con razones trigonométricas en el plano de coordenadas Para poner los ángulos en el plano de coordenadas, esencialmente todo lo que hacemos es mirar las relaciones trigonométricas en términos de X y y valores en vez de frente, adyacente, y hipotenusa. Redefinición de estas proporciones para…
La identificación de la 45 - triángulo de 90 grados - 45 Un 45 a 45 - 90 grados triángulo (o triángulo rectángulo isósceles) es un triángulo con ángulos de 45 # 176-, 176- 45 # y 90 # 176- y los lados de la relación entreTenga en cuenta que se trata de la forma de la mitad de un cuadrado, corte a…
Triángulos trigonométricas básicas Todo por su cuenta, los ángulos son sin duda muy emocionante. Pero los puso en un triángulo, y usted tiene la guinda del pastel. Triángulos son una de las figuras geométricas estudiadas con más frecuencia. Los ángulos que forman el triángulo…
¿Cómo encontrar la inversa de una función trigonométrica Utilice las funciones trigonométricas inversas para resolver ecuaciones como pecado X = 1/2, sec X = -2, O moreno 2X = 1. En las ecuaciones típicas de álgebra, puede resolver por el valor de X dividiendo cada lado de la ecuación por el…