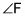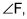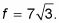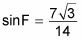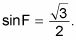Cómo calcular el seno de un ángulo
Porque vas a gastar un montón de tiempo en la pre-cálculo trabajar con funciones trigonométricas, es necesario comprender las proporciones. Una proporción importante de los triángulos rectángulos es el seno. los seno de un ángulo se define como la relación de la pierna opuesta a la hipotenusa. En símbolos, escribes

Esto es lo que la relación se ve así:
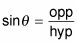
Con el fin de encontrar el seno de un ángulo, debe conocer las longitudes del lado opuesto y la hipotenusa. Usted siempre recibirá las longitudes de dos lados, pero si las dos partes no son los que usted necesita para encontrar una cierta relación, puede utilizar el teorema de Pitágoras para encontrar el que falta. Por ejemplo, para encontrar el seno del ángulo F (pecado F) en la figura, siga estos pasos:

Identificar la hipotenusa.
¿Dónde está el ángulo recto? Es

así lateral r, a través de ella, es la hipotenusa. Usted puede etiquetarlo ". Hyp "
Ubicar el lado opuesto.
Mira el ángulo en cuestión, la cual es
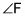
Aquí. ¿De qué lado está al otro lado de ella? Side F es la pierna opuesta. Usted puede etiquetarlo ". Adv "
Etiquetar el lado adyacente.
El único aspecto que queda, lado k, tiene que ser el cateto adyacente. Usted puede etiquetarlo ". Adj "
Localice las dos partes que se utilizan en la relación trigonométrica.
Debido a que usted está encontrando el seno del
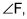
que necesita el lado opuesto y la hipotenusa. Para este triángulo, (pierna)2 + (pierna)2 = (Hipotenusa)2 se convierte en F2 + k2 = r2. Tapón en lo que sabe llegar F2 + 72 = 142. Cuando resuelves esto para f, usted obtiene
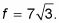
Encuentra el seno.
Con la información de la Etapa 4, se puede encontrar que
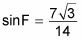
que se reduce a
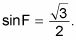
Sobre el autor
 ¿Cómo trabajar con triángulos 30-60-90 grados
¿Cómo trabajar con triángulos 30-60-90 grados Todos los triángulos 30-60-90 grado tienen lados con la misma relación básica. Si nos fijamos en el triángulo 30-60-90 grados en radianes, que se traduce en lo siguiente:En cualquier 30-60-90 triángulo, vea el siguiente:La pierna más corta…
 Trabajar con razones trigonométricas en el plano de coordenadas
Trabajar con razones trigonométricas en el plano de coordenadas Para poner los ángulos en el plano de coordenadas, esencialmente todo lo que hacemos es mirar las relaciones trigonométricas en términos de X y y valores en vez de frente, adyacente, y hipotenusa. Redefinición de estas proporciones para…
 Aplicando el teorema de Pitágoras
Aplicando el teorema de Pitágoras El teorema de Pitágoras se ha conocido durante al menos 2.500 años. Se utiliza el teorema de Pitágoras cuando se sabe las longitudes de dos lados de un triángulo rectángulo y quiere averiguar la longitud del tercer lado.El teorema de…
 Geometría fórmulas y reglas para triángulos
Geometría fórmulas y reglas para triángulos Las pirámides de tres ángulos, bidimensionales conocidos como triángulos son uno de los componentes básicos de la geometría (sin embargo de tres picos que sean). Triángulos, por supuesto, tienen sus propias fórmulas para encontrar el área y…
 Problemas de la práctica de la geometría con triángulos y polígonos
Problemas de la práctica de la geometría con triángulos y polígonos LA polígono es una figura geométrica que tiene al menos tres lados. El triángulo es el polígono más básico. Usted encontrará las siguientes fórmulas y propiedades útiles al responder a las preguntas que implican desigualdades triángulo,…
 Dominios y rangos de funciones trigonométricas
Dominios y rangos de funciones trigonométricas El dominio de una función se compone de todos los valores de entrada que una función puede manejar - la manera que la función está definida. Por supuesto, usted desea conseguir valores de salida (que conforman la gama) cuando introduce valores…
 Encuentra identidades trigonométricas opuesto ángulo
Encuentra identidades trigonométricas opuesto ángulo los identidades de ángulo opuesto cambiar las funciones trigonométricas de ángulos negativos a las funciones de ángulos positivos. Ángulos negativos son grandes para describir una situación, pero no son realmente útil cuando se trata de pegar…
 Cómo determinar la altura de un árbol
Cómo determinar la altura de un árbol ¿Qué función trigonométrica se debe utilizar para determinar la altura de un árbol? Supongamos que usted está volando una cometa, y se ve atrapado en la parte superior de un árbol. Has dejado a cabo los 100 pies de cadena para el kite, y el…
 Cómo utilizar identidades medio ángulo para encontrar el seno de un ángulo
Cómo utilizar identidades medio ángulo para encontrar el seno de un ángulo Mediante la adición, sustracción, o duplicando medidas de los ángulos, se puede encontrar gran cantidad de valores exactos de las funciones trigonométricas utilizando las funciones de ángulos que ya conoce. Por ejemplo, a pesar de que se puede…
 Cómo utilizar la identidad de doble ángulo para el seno
Cómo utilizar la identidad de doble ángulo para el seno La fórmula de doble ángulo para el seno proviene del uso de la identidad trigonométrica para el seno de una suma, el pecado (alfa + beta-) = sinalpha-cosbeta- +-cosalpha sinbeta-. Si alfa = beta-, entonces se puede sustituir beta- con alfa en la…
 Seno y coseno identidades pitagóricas en un círculo unitario
Seno y coseno identidades pitagóricas en un círculo unitario Si alguna vez se preguntó por qué la identidad de Pitágoras, el pecado2theta- + cos2theta- = 1, es tan importante, y de dónde viene, entonces sigue leyendo. Esta identidad es importante porque establece una expresión que involucra funciones…
 La función coseno: adyacente sobre la hipotenusa
La función coseno: adyacente sobre la hipotenusa La función trigonométrica coseno, abreviado cos, funciona mediante la formación de esta relación: adyacente / hipotenusa. En la figura, se ve que los cosenos de los dos ángulos son los siguientes:La situación con las proporciones es el mismo…