Cómo graficar primitivas en la TI-Nspire
Una función tiene un número infinito de primitivas. En el ejemplo dado aquí, nos fijamos en una antiderivada particular, en la TI-Nspire y luego ver cómo utilizar un control deslizante para investigar toda una familia de curvas definidas por una primitiva.
Conteúdo
Utilice la plantilla integral definida TI-Nspire
Para graficar la antiderivada de y = X3 - 3X2 - 2X + 6, siga estos pasos:
Pulse [CTRL] [G] para abrir la línea de entrada, a continuación, el gráfico y = X3 - 3X2 - 2X + 6.
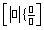
prensa
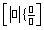
para abrir la plantilla de Matemáticas, resalte la plantilla integral definida, y pulse [ENTER].
Ver la primera pantalla.
Pulse [0] para introducir el límite inferior de la plantilla integral definida, y luego presione [TAB] para pasar al campo de límite superior. Pulse [X] y pulse [TAB] para pasar al campo integral.
Escriba f1 (X) O pulse [VAR] y seleccione f1 de la lista de variables, a continuación, pulse [TAB] de nuevo para pasar al siguiente campo de la plantilla integral definida.
Escribe X en el último campo y pulse [ENTER] para graficar la antiderivada.
Puede tomar unos segundos para que la gráfica para formar en un dispositivo portátil.
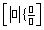
La antiderivada que está graficada aquí se define por la ecuación y = 01.04X4 - X3 - X2 - 6X.
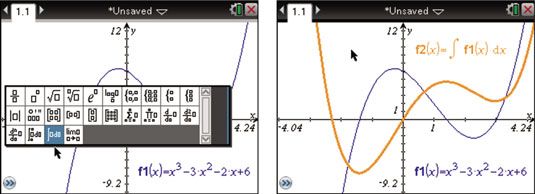
Esta ecuación se basa en la solución general y = 01.04X4 - X3 - X2 - 6X + C con C = 0.
Utilice la plantilla integral indefinida de TI-Nspire CAS
También puede utilizar la TI-Nspire CAS para graficar esta primitiva utilizando la plantilla integral indefinida, también se encuentra en la plantilla de matemáticas se accede pulsando
Para agregar un elemento dinámico, intente insertar un cursor definido por la variable c. Como se muestra en la primera pantalla, utilice la plantilla integral definida para graficar la antiderivada como antes. A continuación, agregue + c en la ecuación para el propósito de investigar la familia de curvas propuesta por el antiderivada de y = X3 - 3X2 - 2X + 6.
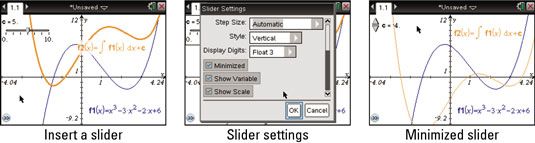
derecha, haga clic en el control deslizante y cambiar la configuración a minimizada (ver la segunda pantalla). Como se ve en la última pantalla, puede hacer clic en el control deslizante y ver la gráfica de la derivada traducir verticalmente.
Evaluar expresiones en TI-Nspire utilizando claves primarias y secundarias Con la TI-Nspire, puede evaluar expresiones matemáticas directamente de la primario teclas (según la definición de las funciones o caracteres situados directamente en las propias claves) y el secundario teclas (según la definición de las…
Evaluar expresiones de TI-Nspire de múltiples maneras Claves de TI-Nspire primarias y secundarias, menú de la aplicación y Catálogo proporcionan una gran cantidad de energía cuando se trabaja en la aplicación de la calculadora. La combinación de todas las teclas y los menús también significa…
Graficar una función de paso en la aplicación gráficas TI-Nspire Muchas funciones pueden ser graficados mediante el acceso a los comandos más utilizados en la aplicación de TI-Nspire Calculadora. los mayor función de número entero, y = Int (X), Es uno de esos gráfico, que se crea siguiendo estos…
Cómo acceder a los comandos utilizados anteriormente en la TI-Nspire TI-Nspire ofrece una manera conveniente de copiar y pegar una expresión con el fin de realizar cálculos similares. Considere que usted desea utilizar la fórmula cuadrática para resolver la ecuación X2 + 3X - 9 = 0. Para empezar, acceda a la…
Cómo crear un gráfico estadístico xy en TI-Nspire En la TI-Nspire, puede crear un X-y parcela estadístico utilizando conjuntos de datos de dos variables. En este documento, el curso y Población EE.UU. datos se introducen en las dos primeras columnas de un Listas La página de la hoja de…
Cómo graficar y actualizar una ecuación de regresión Puede ver la gráfica de una ecuación de regresión en la página de TI-Nspire Gráficos e incluso cambiar los datos y tener la TI-Nspire actualizar la ecuación de forma automática. Para ver el gráfico de la ecuación de regresión, siga estos…
Cómo graficar derivados sobre TI-Nspire El estudio del cálculo debe incluir un enfoque en las cuatro representaciones matemáticas clave: algebraicas, geométricas, numéricas y verbales. La aplicación de TI-Nspire gráficos está dispuesta a hacerse cargo de la representación…
Cómo graficar funciones en la TI-Nspire Funcionalidad integrada en TI-Nspire le permite graficar y analizar funciones, desigualdades, ecuaciones paramétricas, ecuaciones polares, secuencias dinámicas, parcelas de fase, ecuaciones diferenciales, funciones a trozos, y gráficos 3D.prensa…
Cómo graficar desigualdades en la TI-Nspire Con la aplicación de gráficos sobre la TI-Nspire, se puede representar gráficamente una única desigualdad o múltiples desigualdades. Para representar gráficamente una única desigualdad, siga estos pasos, y para graficar varias desigualdades,…
Cómo graficar funciones a trozos en la TI-Nspire prensa [MENU]-Graph Type-Función para cambiar a funcionar el modo de gráficos de la TI-Nspire. Alternativamente, vaya a la línea de entrada y pulse [CTRL] [MENU]-Function. Dos plantillas de función a trozos diferentes están disponibles.La…
Cómo graficar ecuaciones paramétricas en la TI-Nspire prensa [MENU]-Graph Type-paramétrico para cambiar al modo de gráficos paramétricos. Alternativamente, vaya a la línea de entrada y pulse [CTRL] [MENU]-Paramétrico. A continuación, siga estos pasos:Escribe el X-ecuación de componente, usando t…
Comando Integral de TI-Nspire submenú cálculo cas El comando Integral es uno de los comandos más importantes en el submenú de TI-Nspire CAS Cálculo. prensa [MENU]-Cálculo-Integral para abrir la Integral comandos. Una plantilla que contiene cuatro campos se pega a la línea de entrada. Los dos…