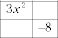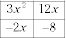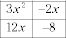Trinomios Factoring utilizando el método de la caja
Un bastante nuevo método o algoritmo, llamado el método de la caja está siendo utilizado para multiplicar dos binomios juntos. Cuando un trinomio de la forma hacha2 + bx + c puede tenerse en cuenta en el producto de dos binomios, el formato de la factorización es (dx + e) (fx + g) dónde d X F = la y e X g = c.
El método de la caja le permite rellenar un cuadrado de dos por dos para crear la factorización deseado. Todavía es necesario conocer los factores de la y c, pero el método de la caja le da un proceso más sistemático para determinar qué factores y términos para elegir.
Un método común para multiplicar los dos binomios juntos se llama FOIL, y la factorización del trinomio resultante se refiere a menudo como unFOIL. En las clases de álgebra tradicionales del método unFOIL fue enseñado, con los estudiantes a encontrar los factores del coeficiente, la, y los factores de la constante, c, y luego rellenar paréntesis para obtener el producto deseado.
A continuación se muestra la factorización de 3X2 + 10X - 8 utilizando el método de la caja.
Dibuja un cuadrado de dos por dos.
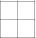
Ponga el primer término del trinomio en la esquina superior izquierda y el último término en la esquina inferior derecha.
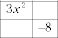
Multiplique el primer y último términos: 3X2(-8) = -24X2.
Encuentra dos factores del producto resultante cuya suma es el término medio, 10X.
Los posibles factores de 24X2 (estos son sin el signo negativo) son X(24X), 2X(12X), 3X(8X), Y 4X(6X).
Usando 2X(12X) Y haciendo que el 2X negativo, tienes -2X(12X) = -24X2. La suma de los dos factores es -2X + 12X = 10X, el término medio del trinomio.
Coloque los factores en los dos cuadrados restantes.
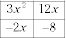
Encuentra el máximo común divisor (MCD) de cada fila y cada columna. Escribe ellos a un lado y por debajo.
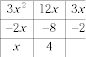
Las dos entradas a lo largo del lado derecho son los términos necesarios en uno de los binomios, y los términos a lo largo de la parte inferior están en la otra factorización. Por lo tanto, 3X2 + 10X - 8 = (3X - 2) (X + 4).
No importa donde se colocan los dos factores en el Paso 5. Si sus posiciones se habían invertido, la plaza se vería así:
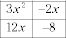
Y los GCFs:
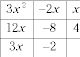
Usted obtiene las mismas entradas para los binomios.
Cómo factorizar un trinomio por unfoiling UnFOILing es un método para factorizar un trinomio en dos binomios. Al multiplicar dos binomios juntos, se utiliza el método FOIL, multiplicando el Frimero, entonces el Outer, entonces la yonner, y finalmente el Ltérminos ast de los dos binomios…
Cómo factorizar expresiones más de una vez A veces se toma expresiones más de una vez - y con diferentes técnicas de factoraje. Para determinar si una expresión debe tenerse en cuenta más de una vez, acaba de tomar otra mirada a la expresión después de que primer factor para ver si…
Cómo multiplicar binomios utilizando el método de lámina de El método FOIL le permite multiplicar dos binomios en un orden determinado. Usted no lo hace tener para multiplicar binomios siguiendo el orden FOIL, pero sí hacer el proceso más fácil. Las letras en FOIL se refieren a dos términos (uno de cada…
¿Cómo reducir fracciones usando factorización prima Puede utilizar factorización prima para reducir fracciones. Comience con sólo números y luego añadir variables (letras que representan cualquier número real) a la mezcla. La belleza de la utilización del método de factorización prima es que…
Cómo desigual grupo de cuatro términos de factoring A veces, en factoring, cuatro términos se pueden separar en grupos irregulares con tres términos en un grupo y un término en el otro. Desigualmente agrupar cuatro términos para el factoring se pueden aplicar a las expresiones donde las…
Cómo escribir descomposición en factores primos de números compuestos Primer factorización le muestra la única manera que un número puede ser un factor. El proceso de descomposición en factores primos se descompone un número compuesto en los números primos que, cuando se multiplica juntos, le dan ese número…
¿Cómo encontrar el máximo común divisor los máximo común divisor (GCF) de un conjunto de números es el mayor número que es un factor de todos esos números. Por ejemplo, el MCD de los números 4 y 6 es 2 porque 2 es el mayor número que es un factor de dos 4 y 6. Aquí aprenderás dos…
Factoring cuatro o más términos agrupando Cuando un polinomio tiene cuatro o más términos, la forma más fácil de factorizar que es usar agrupación. En este método, nos fijamos en sólo dos términos a la vez para ver si cualquiera de las técnicas se hacen evidentes. Por ejemplo,…
Cómo factorizar una diferencia de cuadrados Cuando Foil (multiplicar el primero, afuera, adentro, y último términos juntos) un binomio y su conjugado, el producto se denomina diferencia de cuadrados. El producto de (la - b) (la + b) es la2 - b2. Factoring una diferencia de cuadrados…
Cómo factorizar un cuadrado perfecto FOIL significa multiplicar la primero, afuera, adentro, y último términos juntos. Cuando una lámina de veces binomiales sí mismo, el producto se llama una cuadrado perfecto. Por ejemplo, (la + b)2 le da el trinomio cuadrado perfecto la2 + 2una B…
Cómo factorizar una expresión polinómica En matemáticas, factorización o factorización es la ruptura aparte de un polinomio en un producto de polinomios otros más pequeños. Si lo desea, usted podría entonces multiplicar estos factores juntos, y usted debe obtener el polinomio…
Cómo utilizar el método de papel de aluminio para factorizar un trinomio Para polinomios con un coeficiente de liderazgo no preferenciales y término constante, se puede usar un procedimiento llamado Método FOIL de factoring (a veces llamado el Método británica). El método FOIL siempre trabaja para factorizar…