Cómo factorizar la diferencia de dos cubos perfectos
Para factorizar la diferencia de dos cubos perfectos, recuerde esta regla: la diferencia de dos cubos perfectos es igual a la diferencia de sus raíces cúbicas, multiplicado por la suma de sus cuadrados y el producto de sus raíces cúbicas. El binomio se ve así:
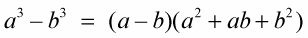
Los resultados de factoring la diferencia de cubos perfectos son
Un factor binomial (la - b) formado por las dos raíces cúbicas de los cubos perfectos separadas por un signo menos.
Si el cubo no está allí, y el número es menor que el más grande de cubo en la lista, entonces el número no es un cubo perfecto. Para los números más grandes, utilizar una calculadora científica y el botón de raíz cúbica.
Un factor trinomio
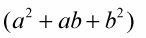
compuestos de los cuadrados de los dos raíces cúbicas añadidos al producto de las raíces de cubo en el centro.
Los cubos perfectos más conocidos son aquellos cuyas raíces son números enteros, no decimales. Familiarizarse con y reconociendo estos cubos en un problema de álgebra puede ahorrar tiempo y mejorar la precisión. Cubos variables son relativamente fáciles de detectar porque sus exponentes son siempre divisible por 3. Si el número está en cubos y se multiplica a cabo, no siempre se puede decir que es un cubo a menos que memorizar una lista de los cubos.
Ejemplo 1: El factor de diferencia entre los cubos, 216-125.
Utilice la diferencia de cubos gobiernan para encontrar las variables.
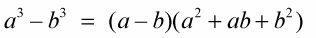
En este caso,
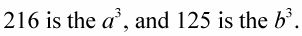
La raíz cúbica de 216 es 6, y la raíz cúbica de 125 es por lo 5- 6 es el la, y 5 es el b.
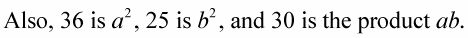
Sustituye los valores en la ecuación.
216-125 = (6 - 5) (36 + 30 + 25).
Compruebe si la ecuación es verdadera.
La diferencia entre 216 y 125 es 91.
También, 6 - 5 = 1, y 36 + 30 + 25 = 91- por lo que (1) (91) = 91.
Si la expresión es la diferencia de los dos cubos o la forma factorizada, la respuesta viene a cabo la misma.
Example 2:
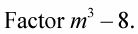
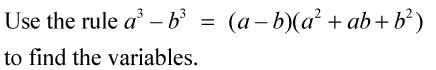
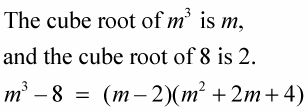
Observe que la señal entre el m y la figura 2 es la misma que la señal entre los cubos.
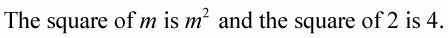
El producto de las dos raíces cúbicas es 2m, y las señales en el trinomio son todos positivos.
Binomios Factoring Si una expresión binomial se puede factorizar en absoluto, debe tenerse en cuenta en una de cuatro maneras. Para decidir qué camino va a utilizar, primero mira en la señal de suma o resta que siempre separa los dos términos dentro del binomio.…
Cómo factorizar un trinomio por unfoiling UnFOILing es un método para factorizar un trinomio en dos binomios. Al multiplicar dos binomios juntos, se utiliza el método FOIL, multiplicando el Frimero, entonces el Outer, entonces la yonner, y finalmente el Ltérminos ast de los dos binomios…
Cómo factorizar la suma de dos cubos perfectos La regla para factorizar la suma de dos cubos perfectos es casi la misma que la regla para factorizar la diferencia entre cubos perfectos. Sólo tienes que cambiar dos pequeñas señales para hacer que funcione. La suma de dos cubos es igual a la…
Cómo factorizar la diferencia de dos cuadrados perfectos Si dos términos en un binomio son cuadrados perfectos separadas por resta, entonces usted puede el factor ellos. Para factorizar la diferencia de dos cuadrados perfectos, recuerde esta regla: si la resta separa dos términos al cuadrado, entonces…
¿Cómo encontrar la diferencia de dos cubos Una expresión que da lugar a la diferencia entre dos cubos suele ser muy difícil de detectar. La diferencia de dos cubos es igual a la diferencia de sus raíces cúbicas veces al trinomio, que contiene los cuadrados de las raíces cúbicas y el…
¿Cómo encontrar la suma de dos cubos Al ver a una distribución que se traduce en la suma de dos cubos es un acceso directo a la solución de los problemas de distribución. Reconocer lo que da como resultado la suma de dos cubos de distribución, mira a ver si la distribución tiene…
Encontrar las raíces de una ecuación factorizada En pre-cálculo, puede utilizar la propiedad del producto cero a encontrar las raíces de una ecuación factorizada. Después se toma un polinomio en sus diferentes piezas, puede configurar cada pieza igual a cero para resolver las raíces con la…
Cómo romper una diferencia cúbica o la suma Después de que se haya registrado para ver si hay un máximo común divisor (MCD) de un polinomio dado y descubrió que es un binomio que no es una diferencia de cuadrados, se debe considerar que puede ser una diferencia o suma de cubos.LA…
Cómo factorizar una diferencia de cuadrados Cuando Foil (multiplicar el primero, afuera, adentro, y último términos juntos) un binomio y su conjugado, el producto se denomina diferencia de cuadrados. El producto de (la - b) (la + b) es la2 - b2. Factoring una diferencia de cuadrados…
Cómo factorizar expresiones matemáticas A menudo se necesita factor expresiones (rompen esas expresiones en sus componentes más simples, o factores) Para el cálculo. Medios de factoring " unmultiplying, " como la reescritura de 12 comoNo encuentras con problemas como que en el cálculo,…
Cómo utilizar las raíces de un polinomio para encontrar sus factores los factor de teorema indica que usted puede ir y venir entre las raíces de un polinomio y los factores de un polinomio. En otras palabras, si usted conoce uno, ya sabes el otro. A veces, su maestro o su libro de texto pueden pedirle que factorizar…
Resolver ecuaciones de trigonometría de factoring El mismo tipo de factoring que el álgebra utiliza para resolver ecuaciones es una gran ayuda en la solución de las ecuaciones de trigonometría. El único truco con las ecuaciones trigonométricas es reconocer que en vez de X's, y's, u otras…
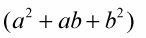
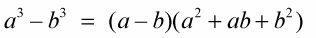
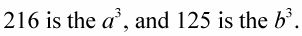
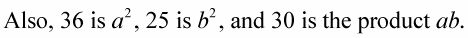
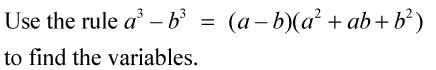
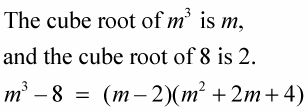