¿Cómo combinar transformaciones con un gráfico de seno o coseno
A veces se le pedirá para graficar una función seno o coseno con más de una transformación. Por ejemplo, puede que tenga que cambiar la amplitud de la gráfica, así como desplazar horizontalmente. Al realizar múltiples transformaciones, debe hacerlo en este orden:
Cambie la amplitud.
Cambie el periodo.
Cambie el gráfico horizontalmente.
Cambie el gráfico verticalmente.
Las ecuaciones que combinan todas las transformaciones en uno son las siguientes:
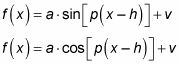
y dividir por p para encontrar el período. La variable h es el desplazamiento horizontal y v es el desplazamiento vertical.
La cosa más importante a saber es que a veces un problema está escrito para que se vea como el período y el desplazamiento horizontal son a la vez dentro de la función trigonométrica. Por ejemplo,
hace que parezca que el período es dos veces más rápido y el desplazamiento horizontal es pi, pero eso no es correcto. Todos los cambios de época debe ser un factor fuera de la expresión para ser realmente los cambios de época, que a su vez revela la verdadera desplazamientos horizontales. Es necesario volver a escribir F(X) Como
Esta función le indica que el período es el doble de rápido, pero que el desplazamiento horizontal es realidad pi / 2 a la derecha.
Debido a que este concepto es tan importante, usted debe buscar en otro ejemplo para asegurarse de que comprenderlo. Con los siguientes pasos, gráfico
Escribe la ecuación en su forma correcta al factorizar el período de constante.
Este paso le da
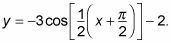
Gráfico El gráfico de los padres.
Grafica la función coseno originales y = Cos X como lo conocen.
Cambie la amplitud.
Esta gráfica tiene una amplitud de 3, pero el signo negativo se vuelve boca abajo '. La gama es ahora [-3, 3]. Usted puede ver el cambio de amplitud en la figura.
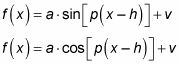Cambio de la amplitud a 3. Desde el coeficiente es -3, el gráfico también se pone de cabeza.Alterar el período.
La constante de medio afecta el periodo. Resolver la ecuación
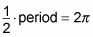
le da el período de
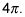
El gráfico se mueve la mitad de rápido y termina en
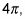
que se puede ver en la figura.
Cambiar el período de 4pi. Un ciclo de la gráfica ahora va desde X = 0 a X = 4pi.Cambie el gráfico horizontalmente.
Cuando factorizado el periodo constante en el paso 1, que descubrió que el desplazamiento horizontal está a la izquierda
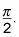
Este cambio se muestra en esta figura.
Un desplazamiento horizontal hacia la izquierda. Un ciclo de la gráfica ahora va desde X = Pi / 2 a X = (7pi) / 2.Cambie el gráfico verticalmente.
Debido a la - 2 que se ve en el paso 1, este gráfico se mueve hacia abajo dos posiciones, que se puede ver en esta figura.
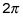
Indique el nuevo dominio y rango.
Las funciones de seno y coseno se definen para todos los ángulos # 952-. El dominio de las funciones seno y coseno son todos los números reales, o
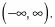
El rango de la gráfica en la figura se ha estirado a causa del cambio de amplitud, y desplazado hacia abajo.
Para encontrar el rango de una función que se ha desplazado verticalmente, agrega o resta el desplazamiento vertical (-2) de la gama alterada sobre la base de la amplitud. Para este problema, el rango de la función coseno transformada es [-3 - 2, 3 - 2], o [-5, 1].
-
Representación gráfica de funciones trigonométricas en pre-cálculo -
¿Cómo cambiar la amplitud, período, y la posición de la tangente o gráfico cotangente -
¿Cómo cambiar la amplitud, período, y la posición de un gráfico secante o cosecante -
Cómo cambiar la amplitud de un gráfico de seno o coseno -
Cómo cambiar el período de un gráfico de seno o coseno -
¿Cómo combinar varias transformaciones
Cómo graficar una función cosecante Cosecante es casi exactamente el mismo que el secante porque es el recíproco de sine (a diferencia de coseno). En cualquier lugar de seno tiene un valor de 0, se ve una asíntota en el gráfico cosecante. Debido a la gráfica cruza el sine X-eje…
Cómo graficar una función coseno El gráfico de matriz de cosenos se ve muy similar a la gráfica de la función de los padres de seno, pero tiene su propia personalidad chispeante (como mellizos). Gráficos coseno seguir el mismo patrón básico y tienen la misma forma básica…
Cómo graficar y transformar una función exponencial Representación gráfica de una función exponencial es útil cuando se desea analizar visualmente la función. Si lo hace, le permite ver realmente el crecimiento o la decadencia de lo que estás tratando. La función madre básica de cualquier…
Cómo graficar una función secante Puede representar gráficamente una función secante F(X) = Sec X mediante el uso de medidas similares a las de tangente y cotangente. Al igual que con tangente y cotangente, la gráfica de la secante tiene asíntotas. Esto es porque secante se…
Cómo graficar funciones parentales y troncos transformados Quieres un poco de buenas noticias, de forma gratuita? Representación gráfica de funciones de los padres y los registros transformadas es muy fácil! Usted puede cambiar cualquier registro en una expresión exponencial, por lo que este paso es lo…
¿Cómo transformar horizontalmente gráficos padres Cuando se aplica un htransformación orizontal a un gráfico padre, usted está estirando o encogiendo el gráfico horizontalmente, a lo largo del X-eje. Un número multiplicar una variable dentro de una función afecta a la posición horizontal del…
Cómo cambiar un gráfico seno o coseno en el plano de coordenadas El movimiento de un seno padre o gráfica coseno alrededor del plano de coordenadas es un tipo de transformación conocido como traducción o una cambio. Para este tipo de transformación, cada punto de la gráfica de los padres se trasladó a otro…
¿Cómo traducir el gráfico de una función Al mover un gráfico horizontal o verticalmente, esto se llama un traducción. En otras palabras, cada punto de la gráfica de los padres se traduce a la izquierda, derecha, arriba o abajo. La traducción siempre implica ningún tipo de adición o…
Ajuste del período de una función seno El período de una función de la trigonometría es la medida de la entrada de los valores que toma para que la función se ejecute a través de todos los valores posibles y empezar todo de nuevo en el mismo lugar para repetir el proceso. En el caso…
Graficar una función seno usando amplitud La función seno y cualquiera de sus variaciones tienen dos características importantes: la amplitud y periodo de la curva. Puede determinar estas características examinado sea la gráfica de la función o su ecuación.los amplitud de la función…
Funciones Gráfico de seno y coseno inversa Las gráficas de las funciones trigonométricas inversas son relativamente singularidad por ejemplo, seno inverso y el coseno inversa son un poco brusca y desarticulada. Estos gráficos son importantes debido a su impacto visual. Especialmente en el…
Funciones Gráfico tangentes con multiplicadores variables En trigonometría, multiplicando el ángulo variable en una función tangente tiene el mismo efecto como lo hace con funciones seno y coseno - que afecta el periodo de la función. Si el múltiplo es 2, como en y = Tan 2X, a continuación, la…