Ajuste del período de una función seno
El período de una función de la trigonometría es la medida de la entrada de los valores que toma para que la función se ejecute a través de todos los valores posibles y empezar todo de nuevo en el mismo lugar para repetir el proceso. En el caso de la función de y = Sen X, el período es de 2pi-, o 360 grados. Escoja cualquier lugar en la curva sinusoidal, siga la curva a la derecha oa la izquierda, y 2pi- o 360 unidades desde su punto de partida a lo largo del X-eje, la curva comienza el mismo patrón de nuevo.
Multiplicando la variable ángulo, X, por un número cambia el período de la función seno. Si se multiplica la variable ángulo por 3, como en y = Sen 3X, entonces la curva hará tres veces más pases completos en la cantidad habitual de espacio. Así multiplicando por 3 realidad reduce la longitud del período. En el caso de
sólo la mitad de la curva se ajusta en el mismo espacio. Así que un coeficiente inferior a 1 aumenta el número de entradas que la función necesita para completar un ciclo.
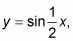
La figura anterior muestra las gráficas de y = Sen 3X y
La ubicación del multiplicador hace una gran diferencia. Multiplicando la función seno por 4 y su variable ángulo por 4 resultados en dos gráficos completamente diferentes. La gráfica de y = 4sin X es mucho más alta de lo habitual - la amplitud es mayor que la de la función seno estándar. La gráfica de y = Sen 4X tiene una amplitud de 1, pero el período es menor y la curva es más arrugó juntos - se repite una y otra vez más rápidamente.
-
Representación gráfica de funciones trigonométricas en pre-cálculo -
Cómo cambiar la amplitud de un gráfico de seno o coseno -
Cómo cambiar el período de un gráfico de seno o coseno -
¿Cómo combinar transformaciones con un gráfico de seno o coseno -
Cómo graficar una función coseno -
Cómo graficar una función seno
Cómo graficar seno, coseno y tangente Así, es necesario graficar un seno, coseno, tangente o función. Seno, coseno y tangente - y sus inversos, cosecante, secante y cotangente - son periódico funciones, lo que significa que sus gráficos contienen una forma básica que se repite una…
La comparación de funciones seno y coseno en un gráfico La relación entre el coseno y seno gráficos es que el coseno es el mismo que el sine - solamente se desplaza a la izquierda en 90 grados, o pi-/ 2. La ecuación de trigonometría que representa esta relación esMira las gráficas de las funciones…
Graficar una función seno usando amplitud La función seno y cualquiera de sus variaciones tienen dos características importantes: la amplitud y periodo de la curva. Puede determinar estas características examinado sea la gráfica de la función o su ecuación.los amplitud de la función…
Funciones Gráfico de seno y coseno inversa Las gráficas de las funciones trigonométricas inversas son relativamente singularidad por ejemplo, seno inverso y el coseno inversa son un poco brusca y desarticulada. Estos gráficos son importantes debido a su impacto visual. Especialmente en el…
Múltiplos gráfica de la función tangente En trigonometría, valores tangentes van desde menos infinito hasta el infinito positivo. Así que cuando usted multiplica toda la función tangente de un número, esto es lo que sucede: Si se multiplica por un número mayor que 1, la función se…
Funciones Gráfico tangentes con multiplicadores variables En trigonometría, multiplicando el ángulo variable en una función tangente tiene el mismo efecto como lo hace con funciones seno y coseno - que afecta el periodo de la función. Si el múltiplo es 2, como en y = Tan 2X, a continuación, la…
Graficar las asíntotas de una función cotangente Las gráficas de la función tangente sientan las bases para las gráficas de la función cotangente. Después de todo, la tangente y cotangente son cofunciones y recíprocos, y tienen todo tipo de conexiones.Las gráficas de estas dos funciones son…
Grafica la función cosecante Una manera muy eficaz de graficar la función cosecante es hacer primero un boceto rápido de la función seno (su recíproco). Con el boceto de seno en su lugar, se puede dibujar las asíntotas de la función cosecante a través de la X-intercepta…
Grafica la asíntota de una función tangente Un asíntota es una línea que ayuda a dar sentido a una gráfica de una función trigonometría. Esta línea no es parte del ficos de la función sino que ayuda a determinar la forma de la curva, mostrando donde la curva tiende a ser una línea…
Variaciones Gráfico en una función secante La gráfica de una función secante es diferente de la cosecante de varias maneras, pero una de las maneras más evidentes es que la gráfica de la secante es simétrica con respecto al y-eje. El secante es un espejo de reflexión sobre ese eje.…
Cómo reconocer los gráficos básicos trigonométricas Las gráficas de las funciones trigonométricas tienen muchas similitudes y muchas diferencias. Los gráficos del seno y el coseno parecen mucho, al igual que la tangente y cotangente, y luego la secante y cosecante tienen similitudes. Pero esos…
Cómo utilizar la identidad de doble ángulo para el seno La fórmula de doble ángulo para el seno proviene del uso de la identidad trigonométrica para el seno de una suma, el pecado (alfa + beta-) = sinalpha-cosbeta- +-cosalpha sinbeta-. Si alfa = beta-, entonces se puede sustituir beta- con alfa en la…