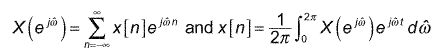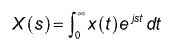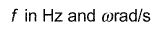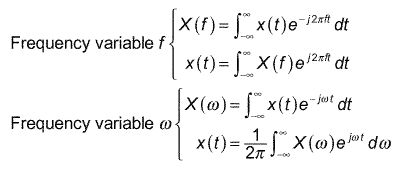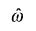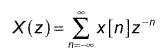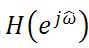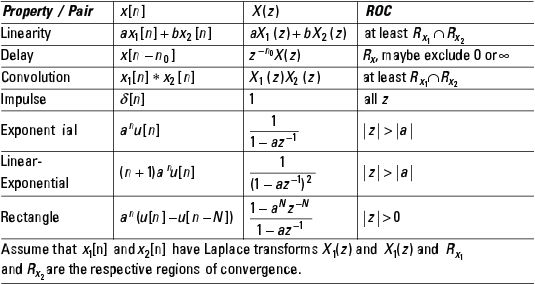El estudio de señales y sistemas establece un formalismo matemático para el análisis, modelado y simulación de sistemas eléctricos en el tiempo, la frecuencia y s
- o
z-dominios. Existen señales de forma natural y también se crean por la gente. Algunos operan de forma continua (conocido como
señales de tiempo continuo) - Los demás están activos en instantes específicos de tiempo (y se denominan
señales de tiempo discreto).
Las señales pasan a través de los sistemas a ser modificadas o mejoradas de alguna manera. Los sistemas que operan en las señales también se clasifican como continuous- o de tiempo discreto.
Matemáticas juega un papel central en todas las facetas de señales y sistemas. Específicamente, compleja aritmética, trigonometría y la geometría son pilares de esto y (ejem) Campo electrizante dinámica de trabajo y estudio. Este artículo destaca los conceptos más pertinentes de cada una de estas áreas de matemáticas para las señales y sistemas de trabajo.
Aritmética Complejo de señales y sistemas
Aquí están algunas de las más importantes operaciones aritméticas complejas y fórmulas que se refieren a las señales y sistemas.
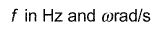
Fórmulas de trigonometría y de Euler
Esta tabla presenta las fórmulas fundamentales de la trigonometría que se aplican a las señales y sistemas:
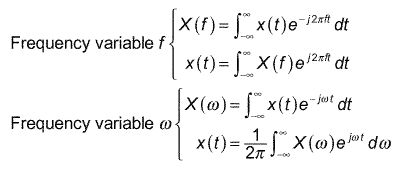
Serie geométrica
Entre las ecuaciones de geometría más importantes que saber para señales y sistemas son estos tres:
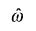
Reconociendo Propiedades y Clasificaciones de señal
Señales - ambas señales de tiempo continuo y sus contrapartes de tiempo discreto - se clasifican de acuerdo a ciertas propiedades, como determinista o aleatorio, periódica o no periódica, el poder o la energía, y el par o impar. Estos rasgos no son mutuamente señales exclusivos- podrás celebrar múltiples clasificaciones.
Estas son algunas de las propiedades de la señal más importantes.
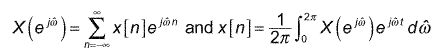
¡Pero espera! Hay más. Las señales también pueden ser categorizados como exponencial, sinusoidal, o una secuencia especial. La secuencia muestra de unidad y de la secuencia de pasos unidad son señales especiales de interés en tiempo discreto. Todas las clasificaciones de señal en tiempo continuo tienen homólogos en tiempo discreto, con excepción de las funciones de singularidad, que aparecen sólo en tiempo continuo.
Definición de las señales especiales que sirven como bloques de construcción para las señales más complejas hace que la creación de modelos de señal personalizada para satisfacer sus necesidades más sistemático y conveniente.
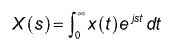
Reconociendo Propiedades y clasificaciones del sistema
Parte de aprender acerca de las señales y sistemas es que los sistemas se identifican de acuerdo con ciertas propiedades que exhiben. Echa un vistazo a las clasificaciones del sistema central:
Linealidad: Una combinación lineal de los resultados obtenidos de forma individual es equivalente a la producción obtenida por el sistema operativo en la correspondiente combinación lineal de los insumos.
Invariante en el tiempo: Las propiedades del sistema no cambian con el tiempo. Un presente de entrada produce la misma respuesta como lo hace en el futuro, menos el factor de cambio de hora entre el presente y el futuro.
Sin memoria: Si la actual salida del sistema depende sólo de la presente entrada, el sistema es sin memoria.
Causal: El actual sistema de salida depende en la mayoría de las entradas presentes y pasados. Las futuras entradas no se pueden utilizar para producir la salida actual.
Estable: Un sistema es-entrada acotada con destino a la producción (BIBO) estable si todas las entradas acotadas producen una salida acotada.
Esta tabla presenta invariantes (LTI) las propiedades del sistema de tiempo lineal básicos para ambos sistemas continuos y discretos. El dominio del tiempo, dominio de la frecuencia, y s/z-propiedades de dominio se identifican para las categorías de entrada / salida, en cascada, de coeficiente lineal constante (LCC) diferenciales y diferencia ecuaciones básicas, y de estabilidad BIBO:
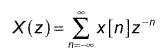
Señales y Sistemas: Trabajar con Transformada de teoremas y pares
Ambas señales y sistemas se pueden analizar en el tiempo-, en frecuencia, y s- y z-dominios. Dejando el dominio del tiempo requiere una transformación y luego una transformada inversa para volver a la dominio de tiempo.
A medida que trabaja desde y hacia el dominio del tiempo, haciendo referencia a las tablas de ambos teoremas transformar y transformar pares pueden acelerar su progreso y hacer el trabajo más fácil. Utilice esta tabla de pares comunes para el tiempo continuo transformada de Fourier en tiempo discreto transformada de Fourier, la transformada de Laplace y el z-transformar según sea necesario.
Trabajar en el dominio de la frecuencia significa que usted está trabajando con transformada de Fourier y de tiempo discreto transformada de Fourier - en el s-dominio.
El uso de transformadas de Fourier para señales de tiempo continuo
He aquí una breve tabla de teoremas y pares para el tiempo continuo transformada de Fourier (FT), tanto en frecuencia variable
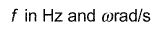
El delantero e inverso transforma para estos dos esquemas de notación se definen como:
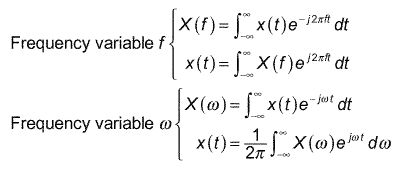
. . . y aquí está la tabla:
La aplicación de la transformada de Fourier de señales de tiempo discreto
Para las señales y sistemas de tiempo discreto del tiempo discreto transformada de Fourier (DTFT) le lleva al dominio de la frecuencia. Una pequeña tabla de teoremas y pares para el DTFT puede hacer su trabajo en este campo mucho más divertido. La variable de frecuencia de tiempo discreto es
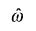
Las transformadas directa e inversa se definen como:
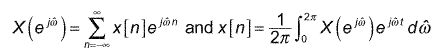
. . . y aquí está la tabla:

Usando la transformada de Laplace en las s-dominio
Para las señales y sistemas en tiempo continuo, el de un solo lado transformada de Laplace (LT) ayuda a descifrar la señal y el comportamiento del sistema. Es también el mejor método para resolver ecuaciones coeficiente constante diferenciales lineales con condiciones iniciales no nulas. El LT de un solo lado se define como:
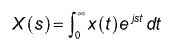
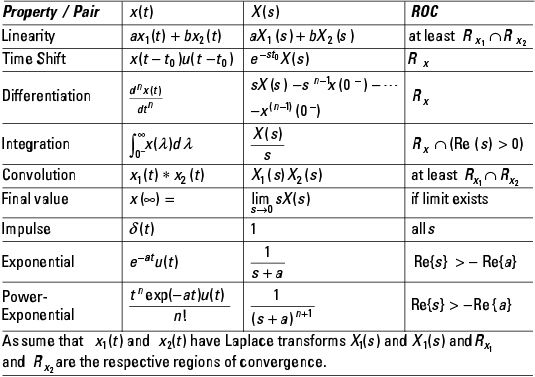
El LT inversa se encuentra típicamente mediante la expansión en fracciones parciales junto con teoremas LT y pares. He aquí una breve tabla de teoremas y pares LT.
Dejar que la ayuda z-Transform con señales y sistemas de análisis
Para las señales y sistemas en tiempo discreto, la z-transformación (ZT) es la contrapartida de la transformada de Laplace. Con la ZT se puede caracterizar señales y sistemas, así como resolver ecuaciones en diferencias coeficiente constantes lineales. El doble cara ZT se define como:
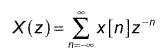
La inversa ZT se encuentra típicamente mediante la expansión en fracciones parciales y el uso de teoremas y pares ZT. He aquí una breve tabla de teoremas y pares ZT.
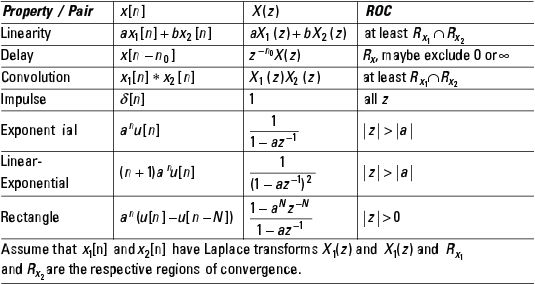
Exploración de Señales y Sistemas: Conceptos básicos de la teoría del muestreo
La teoría del muestreo vincula señales y sistemas en tiempo discreto y continuo. Por ejemplo, se puede obtener una señal de tiempo discreto de una señal de tiempo continuo tomando muestras cada T segundos. Este artículo señala algunas relaciones útiles asociados con la teoría del muestreo. Conceptos clave incluyen el teorema de muestreo de paso bajo, el espectro de frecuencia de una señal continua en el tiempo de muestreo, la reconstrucción utilizando un filtro de paso bajo ideal, y el cálculo de las frecuencias de alias.
La tabla de propiedades comienza con un diagrama de bloques de un subsistema de procesamiento de tiempo discreto que produce una salida de tiempo continuo y(t) Desde la entrada en tiempo continuo X(t). Este diagrama de bloques que motiva a las propiedades de la teoría del muestreo en el resto de la mesa.
El proceso de convertir la señal de tiempo continuo X(t) A tiempo discreto de señales X[n] Requiere de muestreo, que se realiza mediante el bloque (ADC) de analógico a digital. El bloque con una respuesta de frecuencia
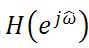
representa un sistema invariante en el tiempo lineal con la entrada X[n] Y la salida y[n]. La señal de tiempo discreto y[n] Se devuelve al dominio de tiempo continuo a través de un convertidor de digital a analógico y un filtro de reconstrucción.

Sintetizando Señales con las Series de Fourier
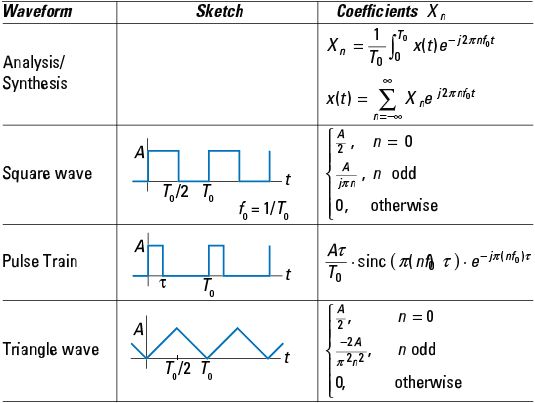
Señales periódicas pueden sintetizarse como una combinación lineal de sinusoides complejas relacionadas armónicamente. La teoría de las series de Fourier proporciona las herramientas matemáticas para esta síntesis comenzando con la fórmula análisis, que proporciona los coeficientes de Fourier Xn correspondiente a señal periódica X(t) Que tiene período T0.
Señales periódicas comunes incluyen la onda cuadrada, tren de pulsos, y onda triangular. Esta tabla muestra los análisis y síntesis de la serie de Fourier fórmulas y fórmulas de coeficientes para Xn en términos de parámetros de forma de onda para los bocetos de forma de onda proporcionadas: