Resolución de ecuaciones diferenciales usando un factor de integración

Un método inteligente para resolver ecuaciones diferenciales (ED) es en la forma de una ecuación lineal de primer orden. Este método implica multiplicar toda la ecuación por una la integración de factor. Una ecuación lineal de primer orden tiene la forma siguiente:

Para utilizar este método, siga estos pasos:

1. Calcular el factor de integración.

2. Multiplique el DE por este factor integrador.

3. Repita el lado izquierdo de la ecuación como un único derivado.

4. Integrar a ambos lados de la ecuación y resuelve para y.

Para ayudarle a entender cómo multiplicar por funciona un factor de integración, la siguiente ecuación está configurado para prácticamente resolverá por sí mismo - es decir, si usted sabe lo que debe hacer:

Observe que este es un primer grado lineal DE, con

y b(X) = 0. Ahora ajustar esta ecuación al multiplicar cada término por X² (que se ve por qué en breve):

A continuación, utiliza el álgebra para hacer un poco de simplificación y reorganización:

Aquí es donde usted aparece para conseguir muy afortunado: Los dos términos en el lado izquierdo de la ecuación acaba de pasar a ser el resultado de la aplicación de la regla del producto a la expresión y # 183- X²:

Observe que el lado derecho de esta ecuación es exactamente el mismo que el lado izquierdo de la ecuación anterior. Así que usted puede hacer la siguiente sustitución:

Ahora, para deshacer el derivado en el lado izquierdo, a integrar ambos lados, y luego a resolver para y:

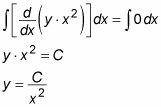
Para comprobar esta solución, se conecta este valor de y de nuevo en la ecuación original:

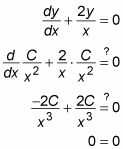
El ejemplo anterior funciona porque has encontrado una manera de multiplicar toda la ecuación por un factor que hizo que el lado izquierdo de la ecuación parece un derivado resultante de la regla del producto. Aunque esto parecía suerte, si usted sabe lo que debe multiplicar por, cada lineal de primer orden DE puede transformarse de esta manera. Recordemos que la forma de un lineal de primer orden DE es la siguiente:

El truco consiste en multiplicar el DE por un factor de integración Residencia en la(X). Aquí está el factor de integración:

Por ejemplo, en el problema anterior, usted sabe que

Así que aquí está la manera de encontrar el factor de integración:

Recuerde que 2 ln X = Ln X², así que:

Como se puede ver, el factor de integración X² es el valor exacto que se multiplica por resolver el problema. Para ver cómo funciona este proceso ahora que usted sabe el truco, aquí hay otro DE resolver:

En este caso, la(X) = 3, por lo que calcular el factor de la integración de la siguiente manera:

Ahora multiplique cada término de la ecuación por este factor:

Si lo desea, utilizar el álgebra para simplificar el lado derecho y reorganizar la parte izquierda:

Ahora se puede ver cómo el lado izquierdo de esta ecuación se parece a la resultado de la Regla del producto aplicado para evaluar la siguiente derivada:

Debido a que el lado derecho de esta ecuación es la misma que el lado izquierdo de la ecuación anterior, se puede hacer la siguiente sustitución:

Observe que cambia el lado izquierdo de la ecuación usando la regla del producto en reversa. Es decir, usted está expresando todo el lado izquierdo como un único derivado. Ahora usted puede integrar ambos lados para cancelar este derivado:

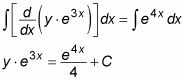
Ahora resolver y y simplificar:

Para comprobar esta respuesta, sustituir este valor de y de nuevo en el DE originales:

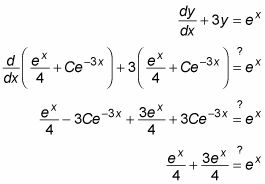
Como por arte de magia, esta respuesta comprueba hacia fuera, así que la solución es válida.