Cómo utilizar la eliminación de Gauss para resolver sistemas de ecuaciones

Eliminación de Gauss es probablemente el mejor método para resolver sistemas de ecuaciones, si usted no tiene un programa de calculadora gráfica o del ordenador para ayudarle.

Las metas de eliminación de Gauss son para hacer que el elemento de la esquina superior izquierda de un 1, utilice las operaciones elementales de fila para conseguir 0s en todas las posiciones por debajo de ese primer 1, obtener 1s para coeficientes de líderes en cada fila en diagonal desde la parte superior izquierda a inferior derecha esquina, y obtener 0s por debajo de todos los principales coeficientes. Básicamente, usted elimina todas las variables en la última fila a excepción de una, todas las variables, excepto para dos en la ecuación anterior que uno, y así sucesivamente y así sucesivamente a la ecuación superior, que tiene todas las variables. A continuación, puede usar otra forma de sustitución para resolver por una variable a la vez conectando los valores que conoces en las ecuaciones de abajo hacia arriba.

Esto se logra mediante la eliminación de la eliminación X (o lo que sea la variable que ocurra primero) en todas las ecuaciones excepto por la primera. A continuación, eliminar la segunda variable en todas las ecuaciones a excepción de los dos primeros. Este proceso continúa, la eliminación de una variable más en cada línea, hasta que sólo una variable se deja en la última línea. Luego resuelve para esa variable.

Puede realizar tres operaciones sobre matrices con el fin de eliminar las variables en un sistema de ecuaciones lineales:

• Usted puede multiplicar cualquier fila por una constante (distinto de cero).

  

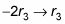
  multiplica la fila tres por -2 para darle una nueva fila tres.

• Puede cambiar cualquiera de las dos filas.

  

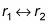
  swaps filas uno y dos.

• Puede agregar dos filas juntos.

  

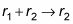
  agrega filas uno y dos y lo escribe en la fila dos.

Incluso puede realizar más de una operación. Usted puede multiplicar una fila por una constante y luego añadirlo a otra fila para cambiar esa fila. Por ejemplo, usted puede multiplicar la fila uno por 3 y luego añadir que a la fila dos para crear una nueva fila dos:

Considere la siguiente matriz aumentada:

Ahora echa un vistazo a las metas de eliminación de Gauss, a fin de completar los siguientes pasos para resolver esta matriz:

1. Completa el primer objetivo: conseguir 1 en la esquina superior izquierda.

   Usted ya lo tienes!

2. Complete el segundo objetivo: conseguir 0s debajo de la 1 en la primera columna.

   Es necesario utilizar la combinación de dos operaciones con matrices juntos aquí. Esto es lo que debe preguntar: "¿Qué necesito para agregar a la fila dos para hacer un 2 convertirse en un 0" La respuesta es -2.

   Este paso se puede lograr mediante la multiplicación de la primera fila por -2 y la adición de la fila resultante a la segunda fila. En otras palabras, realizar la operación

   

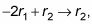
   que produce esta nueva fila:

1. (-2 -4 -6: 14) + (2 -3 -5: 9) = (0 -7 -11: 23)

Ahora tiene esta matriz:

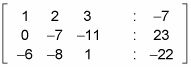
En la tercera fila, consiga un 0 en el marco del 1.

Para hacer este paso, que necesita la operación

Con este cálculo, ahora debería tener la siguiente matriz:

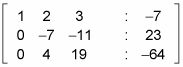
Obtener un 1 en la segunda fila, segunda columna.

Para hacer este paso, es necesario multiplicar por una constante- es decir, se multiplica la fila dos por el recíproco apropiado:

Este cálculo produce una nueva segunda fila:

Get a 0 bajo la 1 que creó en la fila dos.

Volver al buen funcionamiento combo de edad para la tercera fila:

Aquí está otra versión de la matriz:

Obtener otro 1, esta vez en la tercera fila, tercera columna.

Multiplicar la tercera fila por el recíproco del coeficiente para obtener un 1:

Ha completado la diagonal principal después de hacer los cálculos:

Ahora tiene una matriz en forma escalonada, lo que le da las soluciones cuando se utiliza la espalda sustitución (la última fila implica que 0X + 0y + 1z = 4, o z = -4). Sin embargo, si quieres saber como llegar esta matriz en forma escalonada reducida de encontrar las soluciones, siga estos pasos:

1. Obtener un 0 en la fila dos, la tercera columna.

   Multiplicar la fila tres por la constante -11/7 y luego añadiendo filas dos y tres

   

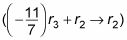
   le da la siguiente matriz:

   

2. Obtener un 0 en la fila uno, la tercera columna.

   La operación

   

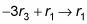
   le da la siguiente matriz:

   

3. Obtener un 0 en la fila uno, la columna dos.

   Por último, la operación

   

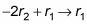
   le da esta matriz:

   

Esta matriz, en forma escalonada reducida, es en realidad la solución del sistema: X = -1, y = 3, y z = -4.