Sistemas exponenciales

Puede resolver sistemas de ecuaciones exponenciales algebraicamente cuando las bases de los términos exponenciales son el mismo número o cuando obvio

(no te odio esa palabra en matemáticas?) soluciones estallar hacia fuera debido a las naturalezas simples de las ecuaciones involucradas. Si las bases son iguales, sólo tiene que establecer los exponentes iguales entre sí.

Cuando una solución algebraica no está disponible, entonces un buen programa de calculadora gráfica o la computadora puede encontrar la solución - que por lo general incluye un montón de valores decimales y / o funciones logarítmicas.

Este artículo trata de los tipos de problemas que se pueden resolver algebraicamente (o simplemente). Por supuesto, la más sencilla es simplemente conectar un número que usted es bastante seguro de obras. Pero ese método puede llevar mucho tiempo si tiene que conectar distancia mucho - se reservan para la cosa segura.

Ejemplos de preguntas

1. Encuentra las soluciones comunes de

   

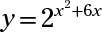
   y y = 16^X+2.

   (2, 65536),

   

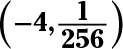
   ¿Quieres las bases a la altura, por lo que primero cambiar el término exponencial en la segunda ecuación para una potencia de 2. Se convierte en y = (2⁴)^{X + 2} = 2^{4X + 8}. Configuración de los dos y-valores de las dos ecuaciones diferentes iguales una a otra, se obtiene

   

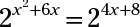
   Ahora configure los dos exponentes iguales entre sí: X² + 6X = 4X + 8. Mover todos los términos a la izquierda y el factoring, X² + 2X - 8 = (X + 4) (X - 2) = 0. Las soluciones de esta ecuación cuadrática son X = -4 O X = 2. Vuelva a colocar la X con -4 en cualquiera de las ecuaciones originales, y se obtiene

   

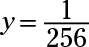
   Reemplazar X con 2 en cualquiera de las ecuaciones, y se obtiene y = 65.536.

2. Encuentra las soluciones comunes de y = 3^{X + 1} y y = 2X + 3

   (0, 3), (-1, 1). Una calculadora gráfica que mostraría una curva exponencial pasando de izquierda a derecha y de una línea que aparece a cortar a través de la curva en dos lugares cerca de la y-eje. Habría que hacer un zoom de cerca para ver los dos puntos de intersección.

   Estas ecuaciones fueron elegidos cuidadosamente para que las respuestas son enteros. Si se evalúa las dos funciones por unos valores, puede determinar las soluciones con el cómputo mínimo.

   Dejar X = 0 en la primera ecuación, y se obtiene y = 3^{0 + 1} = 3. Sea X = 0 en la segunda ecuación, y se obtiene y = 2 (0) + 3 = 3. Una solución! Dejar X = -1 En la primera ecuación, y se obtiene y = 3^{-1 + 1} = 3⁰ = 1. Sea X = -1 En la segunda ecuación, y se obtiene y 2 = (-1) + 3 = -2 + 3 = 1. Estos son los únicos dos soluciones.

Preguntas de práctica

1. Encuentra la solución común (s) de y = 3^{X - 1} y y = 9^X.

2. Encuentra la solución común (s) de y = 8^{2 - X} y

   

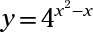
3. Encuentra la solución común (s) de y = 2^X y y = 1 - X.

4. Encuentra la solución común (s) de

   

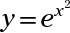
   y y = e.

A continuación se presentan las respuestas a las preguntas de la práctica:

1. La respuesta es

   

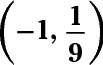
   Set y igual a y para obtener 3^{X - 1} = 9^X. Cambie 9 al 3² y simplificar: 3^{X - 1} = (3²)^X = 3^2X. Ahora que las bases son las mismas, se puede establecer el dos exponentes iguales entre sí y resolver para x: x - 1 = 2x x = -1. Reemplazo de la X con -1 en y = 3^X-1, usted obtiene

   

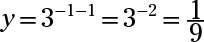
2. La respuesta es

   

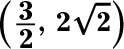
   (-2, 4096).

   En primer lugar, sustituir la expresión exponencial de la primera ecuación para y en el segundo. A continuación, cambie el 8 y 4 para potencias de 2, y simplificar la ecuación:

   

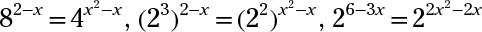
   Las bases son las mismas, por lo que establecen los exponentes iguales entre sí: 6-3X = 2X² - 2X se convierte en 0 = 2X² + X - 6. Factoring, se obtiene 0 = (2X - 3) (X + 2). Cuando

   

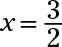
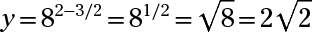
   y cuando X = -2, y = 8^{2 - (- 2)} = 8⁴ = 4.096.

3. La respuesta es (0, 1).

   La primera ecuación es una exponencial que se eleva de manera constante como el X-valores aumentan. La gráfica de la segunda ecuación es una línea que cae constantemente de izquierda a derecha. Se cortan en un único punto. Con algunas selecciones cuidadosas de puntos, se puede determinar rápidamente su solución común única, (0, 1).

   Reemplazo de la X con 0 en la exponencial le da y = 2⁰ = 1. Y la sustitución de la X con 0 en la línea que da y = 1 a 0 = 1.

4. La respuesta es (1, e), (-1, e).

   La función exponencial es positivo para todos los valores de X que de entrada. Y la línea es horizontal, con una y-intersección de (0, e). Si reemplaza el X en el exponencial con 1, se obtiene y = e¹ o y = e. Lo mismo ocurre cuando se reemplaza la X -1- con el cuadrado de -1 es también 1, por lo que se obtiene el mismo y-valor.