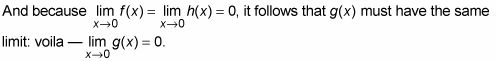¿Cómo resolver límites con un sándwich de límite

Cuando no se puede resolver un límite utilizando el álgebra, trate de hacer un sándwich límite. La mejor manera de entender el emparedado, o apretón, método es mirando un gráfico.

Mira funciones f, g, y h en la figura: g se intercala entre F y h. Si cerca de la X-número - 2 en este ejemplo - F es siempre mayor que o la misma altura que g, y g es siempre mayor que o la misma altura que h, y para que pueda utilizar el teorema del bocadillo:

El límite de ambos F y h como X enfoques 2 es 3. Por lo tanto, 3 tiene que ser el límite de g así como. Tiene otro lugar adonde ir. He aquí otro ejemplo:

1. Trate de sustitución (siempre trato de sustitución primero).

   

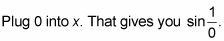
   No es bueno, no se puede dividir por cero. En al plan B.

2. Trate métodos algebraicos o cualquier otros trucos que tiene bajo la manga.

   Noquearse. No puede hacerlo. Plan de C.

3. Pruebe la calculadora.

   (Nota: las instrucciones Calculadora siguientes son para una calculadora gráfica como el modelo TI-84 o similar, pero si se utiliza otra marca de la calculadora gráfica, usted debería ser capaz de lograr los mismos resultados..)

   Siempre es una buena idea para ver lo que su calculadora te dice, incluso si se trata de un " mostrar su trabajo " problema. Para graficar esta función, ajuste el modo de su calculadora gráfica para radián y la ventana para

4. X min = -0.4

5. X max = 0,4

6. y min = -0.3

7. y max = 0,3

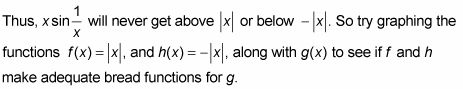
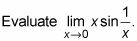
La siguiente figura muestra lo que la gráfica se parece.



Definitivamente parece que el límite de g como es cero X se aproxima a cero por la izquierda y la derecha. Ahora, compruebe la tabla de valores en tu calculadora (juego TblStart a 0 y # 8710-Tbl a 0.001). La siguiente tabla muestra algunos de los valores de la tabla que aparecerán en tu calculadora.



X	g(X)
0	Error
.001	.0008269
.002	-.000.936
.003	.0009565
.004	-.003.882
.005	-.004.366
.006	-.000.969
.007	-.006.975
.008	-.004.928
.009	-.008.234

Estos valores de la función especie de parecer que están cada vez más cerca de cero como X se acerca a cero, pero no están convenciendo (nótese que cuando X se acerca a cero 0,006 a 0,005, g obtiene más lejos de cero). Este tipo de tabla (utilizando el automático # 8710-Tbl) No funciona tan grande para hacer oscilar funciones como seno o coseno. Así que trate el tipo de tabla se describe a continuación.

Escriba la función en la pantalla de inicio de tu calculadora y conecte sucesivamente en la X-valores listados en la siguiente tabla para obtener los valores de la función correspondiente.



X	g(X)
.1	-.054
.01	-.0051
.001	.00083
.0001	-.000031
.00001	.00000036

Ahora definitivamente se puede ver que g se dirigió hacia cero a medida X se aproxima a cero.

8. Ahora tiene que demostrar el límite matemáticamente, a pesar de que ya se ha resuelto en su calculadora. Para ello, es necesario hacer un sándwich límite.

   La parte difícil de usar el método sándwich viene con el " pan " funciones (de nuevo, funciones F y h son el pan y g es el salami). No hay forma automática de hacer esto. Tienes que pensar en la forma de la función salami, y luego utilizar su conocimiento de las funciones y su imaginación para llegar a algunas buenas perspectivas para las funciones de pan.

   Debido a que el rango de la función sinusoidal es de negativo a positivo 1 1, cada vez que multiplicar un número por el seno de cualquier cosa, el resultado ya sea se mantiene la misma distancia de cero a medida que se acerca o número a cero.

   

   La siguiente figura muestra lo que hacen.

   

Has demostrado - aunque tal vez no con la satisfacción de un matemático, egad! - ese

F (X) # 8805- g (X) # 8805- h (X).