Aplicar la función exponencial para el análisis de circuitos
los funcion exponencial es una función escalón cuya amplitud Vk disminuye gradualmente a 0. Las funciones exponenciales son importantes para el análisis de circuitos porque son soluciones a muchos problemas en el que un circuito contiene resistencias, condensadores, e inductores.
La forma de onda exponencial se describe por la siguiente ecuación:
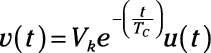
La constante de tiempo TC proporciona una medida de la rapidez con la función decaerá o crecer. Utilizando la función de paso significa que la función empieza a las t = 0.
El signo menos en el exponente indica un decaimiento exponencial, mientras que un signo positivo indica un crecimiento exponencial. Cuando usted tiene un crecimiento exponencial, el circuito no puede manejar la entrada, y nada funciona después de exceder la tensión suministrada. En términos académicos, el sistema va inestable.
Aquí está la versión en diferido de un partida exponencial en descomposición en el tiempo t0:
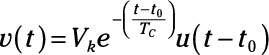
Aquí está una exponencial en descomposición, su versión en diferido y un exponencial crecimiento.
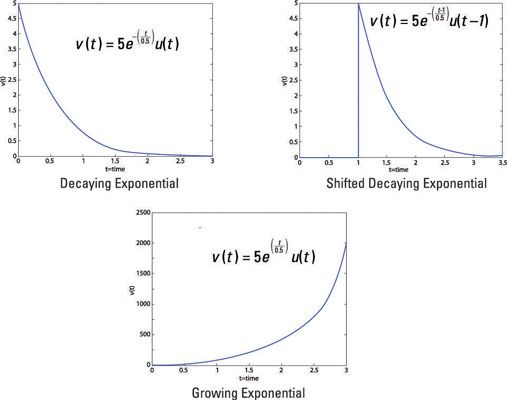
Hay otras funciones útiles para el análisis de circuitos, además de la función exponencial. Estas funciones incluyen la función escalón unitario, la función de impulso, y las funciones sinusoidales. Además, la fórmula de Euler conecta funciones trigonométricas con funciones exponenciales complejas.
Cómo interpretar las gráficas de funciones Vas a ver a decenas y decenas de funciones en su estudio del cálculo, y las gráficas de estas funciones puede expresar visualmente las cosas tales como la inflación, el crecimiento demográfico y la desintegración radiactiva. A continuación se…
¿Cómo resolver una ecuación exponencial con una variable en uno o ambos lados Ya sea una ecuación exponencial contiene una variable en uno o ambos lados, el tipo de ecuación se le pide resolver determina los pasos que se dan para resolverlo.El tipo básico de la ecuación exponencial tiene una variable en un solo lado y se…
Cómo utilizar fasores para el análisis de circuitos LA phasor es un número complejo en forma polar que se puede aplicar al análisis de circuitos. Al trazar la amplitud y la fase de cambio de una sinusoide en un plano complejo, se forma un vector de fase, o fasor.Como usted puede recordar de la…
Resolver funciones compuestos donde la función interna es hacha Al calcular problemas de Cálculo, algunas integrales de funciones compuestos F (g(X)) Son fáciles de hacer rápidamente. Estos incluyen funciones compuestos para los que saben cómo integrar la función externa F, y la función interna g(X) Es de…
¿Cómo encontrar la inversa de una función trigonométrica Utilice las funciones trigonométricas inversas para resolver ecuaciones como pecado X = 1/2, sec X = -2, O moreno 2X = 1. En las ecuaciones típicas de álgebra, puede resolver por el valor de X dividiendo cada lado de la ecuación por el…
Aplique la función escalón unitario para el análisis de circuitos Los escalón unitario (Heavyside) modelos de función de la conducta de un interruptor (encendido / apagado). La función escalón unidad puede describir los cambios bruscos de corriente o voltaje en un circuito. La función escalón unitario se…
Describir los circuitos de segundo orden con ecuaciones diferenciales de segundo orden Si usted puede utilizar una ecuación diferencial de segundo orden para describir el circuito que está viendo, entonces usted está tratando con un circuito de segundo orden. Circuitos que incluyen un inductor, condensador y resistencia conectada…
Cómo detectar un impulso faltante con un circuito de temporización Cuando el tiempo es apagado en su ordenador, eventos específicos no se presentan en el orden correcto. Pero si usted sabe la física y yo-v relaciones de resistencias y condensadores, puede crear un circuito que pulses- detecta a continuación,…
Análisis de S-dominio: la comprensión de polos y ceros de f (s) Transformadas de Laplace se pueden utilizar para predecir el comportamiento de un circuito. La transformada de Laplace toma una función de dominio de tiempo f (t), y la transforma en la función F (s) en el s-dominio. Puede ver las transformadas de…
Funciones sinusoidales y análisis de circuitos Las funciones sinusoidales (seno y coseno) aparecen por todas partes, y juegan un papel importante en el análisis de circuitos. Las funciones sinusoidales proporcionan una buena aproximación para describir la entrada de un circuito y el…
Analizar un circuito RL paralelo usando una ecuación diferencial Un primer orden circuito en paralelo RL tiene una resistencia (o de la red de resistencias) y un único inductor. Circuitos de primer orden pueden ser analizadas usando las ecuaciones diferenciales de primer orden. Mediante el análisis de un…
Encuentra las respuestas de entrada cero y por el estado cero de un circuito RC serie Para encontrar la respuesta total de un circuito RC en serie, es necesario encontrar la respuesta a entrada cero y la respuesta de estado cero y luego sumarlos. Un circuito en serie RC de primer orden tiene una resistencia (o de la red de…