Funciones sinusoidales y análisis de circuitos

Las funciones sinusoidales (seno y coseno) aparecen por todas partes, y juegan un papel importante en el análisis de circuitos. Las funciones sinusoidales proporcionan una buena aproximación para describir la entrada de un circuito y el comportamiento de la producción no sólo en ingeniería eléctrica, pero en muchas ramas de la ciencia y la ingeniería.

La función sinusoidal es periódica, es decir, su gráfica contiene una forma básica que se repite una y otra vez indefinidamente. La función continúa para siempre, oscilando a través de picos y valles interminables en ambas direcciones positivas y negativas de tiempo. Estas son algunas de las piezas clave de la función:

• La amplitud V_LA define los picos máximos y mínimos de las oscilaciones.

• Frecuencia F₀ describe el número de oscilaciones en 1 segundo.

• El período T₀ define el tiempo necesario para completar 1 ciclo.

El período y la frecuencia son recíprocos el uno del otro, que se rige por la siguiente relación matemática:

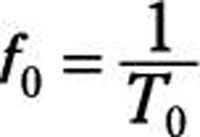
Aquí es una función coseno se puede utilizar como la señal de referencia:

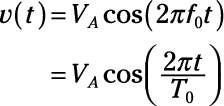
Puede mover funciones sinusoidales izquierda o derecha con un cambio de tiempo, así como aumentar o disminuir la amplitud. También puede describir una función sinusoidal con un desplazamiento de fase en términos de una combinación lineal de funciones seno y coseno. Aquí es una función coseno y una función coseno desplazado con un desplazamiento de fase de # 960- / 2.

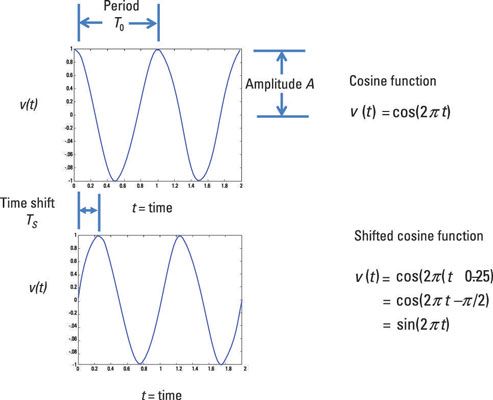
Desplazamientos de fase en una función sinusoidal

Una señal de que es fuera de fase se ha desplazado izquierda o la derecha cuando se compara con una señal de referencia:

• Desplazamiento a la derecha: Cuando una función mueve a la derecha, entonces la función se dice que es retrasado. El coseno retraso tiene su pico se produce después de que el origen. Una señal retardada también se dice que es una señal de retardo debido a que la señal llega más tarde de lo esperado.

• Shift izquierdo: Cuando la función coseno se desplaza a la izquierda, la función desplazado se dice que es avanzado. El pico de la señal avanzada se produce justo antes del origen. Una señal avanzada también se denomina señal de plomo debido a que la señal de plomo llega antes de lo esperado.

Estos son ejemplos de funciones coseno no está cambiada rezagado, y plomo.

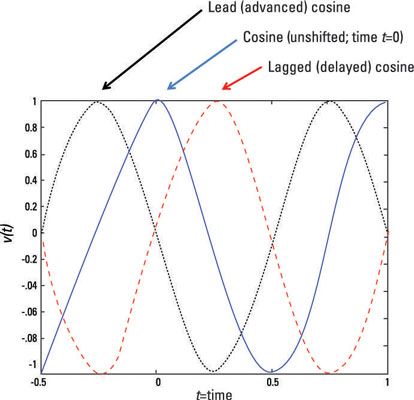
Para ver lo que un desplazamiento de fase parece matemáticamente, primero echar un vistazo a la señal de referencia:

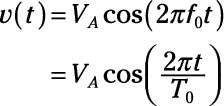
A t = 0, el pico positivo V_LA sirve como punto de referencia. Para mover el punto de referencia por el cambio de hora T_S, Reemplace la t con (t - T_S):

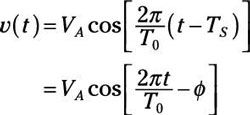
dónde

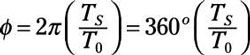
El factor # 981- es el cambio de fase (o ángulo). El desplazamiento de fase es el ángulo entre t = 0 y el pico positivo más cercano. Puede ver la ecuación anterior como la representación polar de la sinusoide. Cuando el desplazamiento de fase es # 960- / 2, entonces el coseno desplazado es una función sinusoidal.

Expresar el ángulo de fase en radianes para asegurarse de que está en las mismas unidades que el argumento del coseno (2 # 960-t/T₀ - # 981-). Los ángulos se pueden expresar, ya sea en radianes o grados- asegúrese de usar la configuración de la calculadora a la derecha.

Cuando usted tiene un desplazamiento de fase # 981- en la salida cuando se compara con la entrada, por lo general es causada por el propio circuito.

Expandir una función sinusoidal y encontrar coeficientes de Fourier

La sinusoide en general v (t) implica el coseno de la diferencia de ángulos. En muchas aplicaciones, puede ampliar la sinusoide en general mediante la siguiente identidad trigonométrica:

La ampliación de la sinusoide en general v (t) lleva a

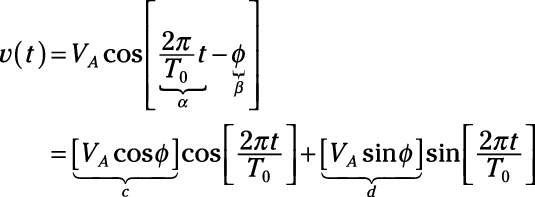
Los términos c y d son constantes acaba especiales llamadas Coeficientes de Fourier. Usted puede expresar la forma de onda como una combinación de senos y cosenos de la siguiente manera:

La funcion v (t) describe una señal sinusoidal en forma rectangular.

Si conoces a tus números complejos que va entre las formas polares y rectangulares, entonces usted puede ir entre las dos formas de los sinusoides. Los coeficientes de Fourier c y d están relacionadas por la amplitud V_LA y la fase # 981-:

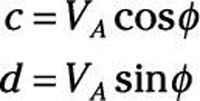
Si vuelves a encontrar V_LA y # 981- a partir de los coeficientes de Fourier c y d, que terminan con estas expresiones:

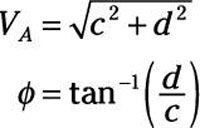
La función tangente inversa en una calculadora tiene un positivo o negativo 180 # 176- (o # 960-) ambigüedad de fase. Puede averiguar la fase observando los signos de los coeficientes de Fourier c y d. Dibuja los puntos c y d en el sistema rectangular, donde c es el X-componente (o abscisa) Y d es el y-componente (o ordenada).

La relación de d/c puede ser negativo en los cuadrantes II y IV. Utilizando el sistema rectangular le ayuda a determinar los ángulos de la hora de tomar el arcotangente, cuyo rango es de - # 960- / 2 a # 960- / 2.

Conecte funciones sinusoidales a exponenciales con la fórmula de Euler

La fórmula de Euler conecta funciones trigonométricas con funciones exponenciales complejas. La fórmula establece que para cualquier número real # 952-, dispone de las siguientes expresiones exponenciales complejos:

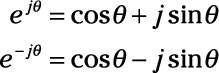
El exponente j# 952- es un número imaginario, donde j = # 8730 a -1.

El número imaginario j es el mismo que el número yo de sus clases de matemáticas, pero toda la gente fresca utilizan j para los números imaginarios PORQUE yo representa actual.

Puede sumar y restar las dos ecuaciones anteriores para obtener las siguientes relaciones:

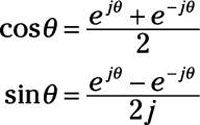
Estas ecuaciones dicen que las funciones coseno y seno se construyen como una combinación de exponenciales complejas. Los exponenciales complejos juegan un papel importante cuando se está analizando circuitos complejos que tienen dispositivos de almacenamiento tales como condensadores e inductores.