Cómo utilizar fasores para el análisis de circuitos

LA phaso

r es un número complejo en forma polar que se puede aplicar al análisis de circuitos. Al trazar la amplitud y la fase de cambio de una sinusoide en un plano complejo, se forma un vector de fase, o fasor.

Como usted puede recordar de la clase de álgebra, un número complejo se compone de una parte real y una parte imaginaria. Para el análisis de circuitos, pensar en la parte real como la vinculación con resistencias que deshacerse de la energía en forma de calor y la parte imaginaria como en relación con la energía almacenada, como el tipo que se encuentra en inductores y condensadores.

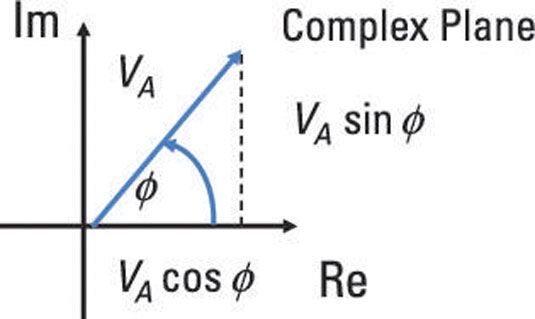
También puede pensar en un fasor como un vector de rotación. A diferencia de un vector que tiene magnitud y dirección, un fasor tiene magnitud V_LA y φ desplazamiento angular. Se mide el desplazamiento angular en la dirección en sentido antihorario desde el eje x positivo.

Este es un diagrama de un fasor de voltaje como un vector que gira a cierta frecuencia, con su cola en el origen. Si necesita añadir o restar fasores, puede convertir el vector en su X-componente (V_LA cos φ) Y es y-componente (V_LA φ pecado) Con un poco de trigonometría.

Las siguientes secciones explican cómo encontrar las diferentes formas de fasores y le presentaremos a las propiedades de los fasores.

Encontrar formas de fasores

Los fasores, que usted describe con números complejos, encarnan la amplitud y fase de una tensión sinusoidal o actual. La fase es el desplazamiento angular de la sinusoide, lo que corresponde a un cambio de hora t₀. Así que si tienes cos [omega-(t - t₀)], después omega-t₀ = Φ_O, dónde φ_O es el desfase angular.

Para establecer una conexión entre los números complejos y de seno y coseno olas, necesita la exponencial compleja e^jtheta- y la fórmula de Euler:

e^jtheta- = Costheta- + jpecadotheta-

dónde

j = Radic - 1

El lado izquierdo de la fórmula de Euler es la polar forma fasorial, y el lado derecho es la forma fasorial rectangular. Usted puede escribir el coseno y seno de la siguiente manera:

costheta- = Re [e^jtheta-]pecadotheta- = Im [e^jtheta-]

En las ecuaciones que se muestran aquí, Re [] denota la parte real de un número complejo, y Im [] denota la parte imaginaria de un número complejo.

Aquí es una función coseno y una función coseno desplazado con un desplazamiento de fase de PI / 2.

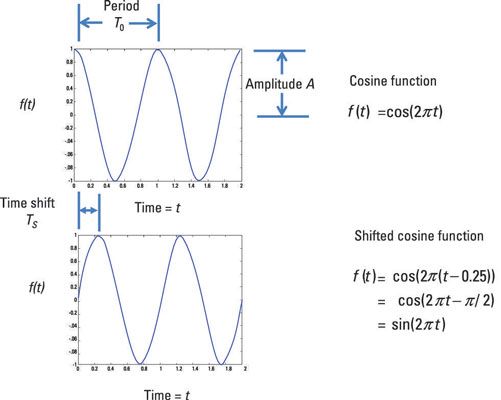
En general, para los sinusoides muestran aquí, usted tiene una amplitud V_LA, una frecuencia en radianes omega-, y un desplazamiento de fase de φ dada por la siguiente expresión:

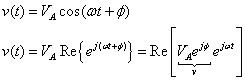
Debido a que la frecuencia en radianes omega- sigue siendo la misma en un circuito lineal, un fasor sólo necesita la amplitud V_LA y la fase φ para entrar en forma polar:

V = V_LAe^jφ

Para describir un fasor, necesita sólo la amplitud y el desplazamiento de fase (no la frecuencia en radianes). Utilizando la fórmula de Euler, la forma rectangular del fasor es

V = V_LAcosφ + j V_LApecadoφ

Examine las propiedades de fasores

Una propiedad fasor clave es la propiedad aditiva. Si agrega sinusoides que tienen la misma frecuencia, a continuación, el fasor resultante es simplemente la suma vectorial de los fasores - al igual que la adición de vectores:

V = V₁ + V₂ + ...V_N

Para esta ecuación para trabajar, fasores V₁, V₂, ...,V_N debe tener la misma frecuencia. Usted encuentra esta propiedad útil cuando se utilizan las leyes de Kirchhoff.

Otra propiedad fasor vital es la derivada temporal. La derivada en el tiempo de una onda sinusoidal es otra onda sinusoidal ajustada a escala con la misma frecuencia. Tomando la derivada de fasores es una multiplicación algebraica de jomega- en el dominio fasorial. En primer lugar, se relaciona el fasor de la onda sinusoidal original al fasor de la derivada:

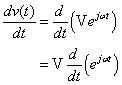
Pero la derivada de una exponencial compleja es otro exponencial multiplicado por jomega-:

Sobre la base de la definición de fasores, la cantidad (jomega-V) Es el fasor de la derivada temporal de un fasor de onda sinusoidal V. Vuelva a escribir el fasor jomega-V como

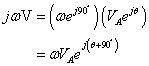
Al tomar la derivada, se multiplica la amplitud V_LA por omega- y cambiar el ángulo de fase por 90^o, o equivalentemente, se multiplica la onda sinusoidal original jomega-. Ver cómo el número imaginario j gira por un fasor 90^o?

Trabajar con condensadores e inductores implica derivados porque las cosas cambian con el tiempo. Para los condensadores, la rapidez a los cambios de voltaje condensador dirige la corriente del condensador. Para inductores, la rapidez con un inductor cambios actuales controla la tensión de inductor.