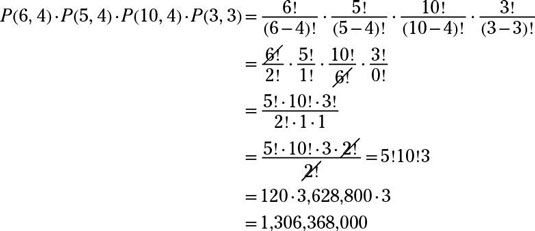Permutaciones cuando los asuntos de orden

Permutaciones

involucrar a tomar un número específico de elementos de un grupo de disposición o conjunto y ver cómo muchas maneras diferentes los elementos se pueden seleccionar y luego arreglar.

Por ejemplo, si elige tres cartas del conjunto {la, r, s, t} Y las presenta de tantas maneras como sea posible, a obtener los arreglos de {la, r, s}: ars, asr, ras, rsa, sar, y sra- los arreglos de {la, r, t}: arte, atr, rata, rta, alquitrán, y tra- y los arreglos de {la, s, t}: ast, ats, sáb, sta, tas, y tsa- y los arreglos de {r, s, t}: primera, rts, srt, str, trs, y tsr.

El número de permutaciones es 24.

Si se pierde la pista de cómo averiguar toda la " es decir, " usted puede enumerar todos estos acuerdos mediante una árbol. Sin un árbol, simplemente encontrar una manera de hacer una lista sistemática.

Usted puede encontrar el número de permutaciones de n cosas toman r a la vez con la fórmula

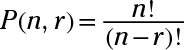
los n es la agrupación o conjunto que está tirando de los artículos en. los r es cuántos de esos artículos que usted está tomando a la vez. La notación P(n, r) O _nP_r es la notación estándar para indicar permutaciones.

Ejemplos de preguntas

1. 1.¿Cuántas permutaciones son posibles si elige tres cartas de un conjunto de cuatro?

   24. Utilizando la fórmula,

   

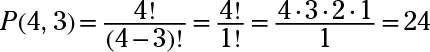
2. 2.¿Cuántos arreglos son posibles si elige cualquiera de las tres letras del alfabeto Inglés y luego tomar cualquiera de los tres dígitos de los dígitos del 0 al 9 y usarlos para una contraseña (suponiendo que ninguno se repite)?

   11232000. En primer lugar, utilice la fórmula para encontrar el número de arreglos de letras:

   

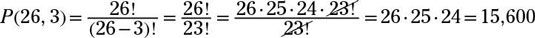
   A continuación, busque el número de arreglos de dígitos:

   

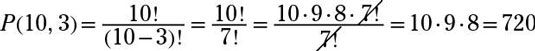
   Por último, se multiplican las dos respuestas juntos: 15.600 x 720 = 11232000.

Preguntas de práctica

1. ¿Cuántos arreglos (" palabras ") son posibles con tres de las letras de la palabra mirar?

2. ¿Cuántos arreglos (" palabras ") son posibles con los cinco de las letras de la palabra mirar?

3. ¿Cuántas placas puede formar usando tres letras del alfabeto Inglés (excepto las letras O y yo y no repetir lo hay), dos dígitos de los dígitos 1 a 9 (sin repetición), y luego dos letras elegidas desde los primeros siete letras en el alfabeto (no dos de la misma letra)?

4. Tiene seis libros azules, cinco libros rojos y diez libros verdes, y usted decide poner cuatro de cada color en una estantería, manteniendo los mismos colores juntos. ¿Cuántos arreglos son posibles?

A continuación se presentan las respuestas a las preguntas de la práctica:

1. La respuesta es 60.

   Use la fórmula de permutación P(5, 3). Simplificando,

   

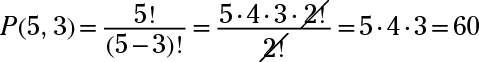
2. La respuesta es 120.

   Use la fórmula de permutación P(5, 5). Simplificando,

   

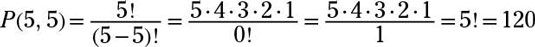
3. La respuesta es 36723456.

   Utilice tres permutaciones diferentes de todo multiplicados juntos. Para las tres primeras letras, el uso P(24, 3). Los dos dígitos utilizan P(9, 2). Y las dos últimas letras utilizan P(7, 2):

   

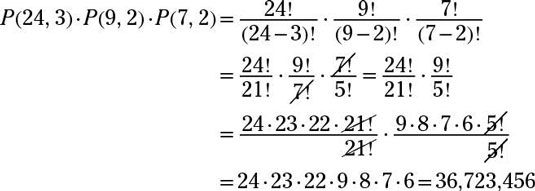
4. La respuesta es 1306368000.

   Utilice cuatro permutaciones diferentes de todo multiplicados juntos. Para los libros azules, el uso P(6, 4) - para los libros rojos, el uso P(5, 4) - y por los libros verdes, el uso P(10, 4). A continuación, tiene que dar cuenta de lo que ordenan los tres colores van a ser. Utilice P(3, 3). Los libros se ordenarán dentro de sus colores y de los grupos de colores se pueden pedir. ¡Menos mal! Esto es lo que se ve el trabajo como: