Cómo utilizar combinaciones de factor probabilidades binomiales
En la fórmula binomial, se utiliza la fórmula de combinaciones para contar el número de combinaciones que se pueden crear en la elección X objetos de un conjunto de n objetos:
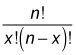
Una característica distintiva de una combinación es que el orden de los objetos es irrelevante.
Por ejemplo, puede utilizar esta fórmula para contar el número de maneras que usted elija dos clases electivas de un conjunto de ocho para el próximo semestre. El orden en que usted elige las asignaturas optativas es inmateriales- cada posible selección es un combinación de dos objetos.
Como otro ejemplo, supongamos que usted está pintando su casa con dos colores de un conjunto de cuatro: verde, azul, blanco y amarillo. Debido a que el orden en el que usted elige los colores es irrelevante, cada par de colores es una combinación. ¿Cuántas combinaciones de colores diferentes son posibles con el conjunto determinado de opciones? Usted puede responder a esta pregunta por simple enumeración de todas las combinaciones posibles:
verde, blancoverde azulverde amarilloblanco, amarilloblanco, azulazul, amarillo
Esta lista muestra que usted tiene seis posibles opciones de pares de colores.
La manera más rápida de responder a esta pregunta es sustituir estos valores en las combinaciones formulación en este caso, X representa el número de colores a elegir (2), y n representa el número total de colores que puede elegir (4).
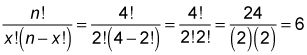
La fórmula para calcular el número de combinaciones se expresa a veces como
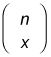
Leer o decir esta expresión como "n escoger X."Esta función aparece en muchas calculadoras como NCR. En Microsoft Excel, puede calcular combinaciones con el COMBINAT función.
Cuando usted está seleccionando X objetos a partir de un grupo de n objetos de tal manera que el orden de selección no importa, las decisiones se conocen como permutaciones en lugar de combinaciones.
-
Cómo añadir color a gráficos de Fireworks CS5 -
Cuadros de mando e informes de Excel: Ejemplo de cuadro de lista -
¿Cómo crear una combinación de colores personalizada en PowerPoint 2013 -
Estudio Manga atajos de teclado - Electrónica componentes: valores de resistencia estándar
-
Electrónica puertas lógicas: y portones
Permutaciones, combinaciones y números aleatorios en la TI-83 Plus Puede utilizar la TI-83 Plus para evaluar una permutación o combinación. LA permutación, denotado por nPr, responde a la pregunta: " De un conjunto de n diferentes artículos, cuántas maneras se puede seleccionar y fin (organizar) r de estos…
Permutaciones y combinaciones y la TI-84 Plus Puede trabajar permutaciones y combinaciones en el Plus calculadora TI-84. LA permutación, denotado por nPr, responde a la pregunta: " De un conjunto de n diferentes artículos, cuántas maneras se puede seleccionar y fin (organizar) r de estos…
Cómo pronunciar vocales combinados en francés Varias combinaciones de vocales son posibles en francés: dos o tres vocales juntas o una vocal y una consonante. Pero cada vez que el sonido que se produce es un sonido vocal, incluso cuando se incluye una consonante.Cómo pronunciar combinaciones…
Posición pronombres francés en frases que necesitan dos pronombres A veces es necesario utilizar dos pronombres franceses en la misma frase, como para responder Como-tu mal les livres sur le bureau? (¿Pusiste los libros sobre la mesa?): Oui, je les y ai mal (Sí, me los puse allí).Con dos pronombres, tiene varias…
Combinaciones algebraicas Las combinaciones son otra manera de contar las cosas. Esta vez, seleccionar algunos elementos de un grupo más grande, pero no me importa qué orden vienen en. Por ejemplo, si selecciona 6 números de la lotería de una lista de 54, cuyo número…
Permutaciones cuando los asuntos de orden Permutaciones involucrar a tomar un número específico de elementos de un grupo de disposición o conjunto y ver cómo muchas maneras diferentes los elementos se pueden seleccionar y luego arreglar.Por ejemplo, si elige tres cartas del conjunto…
Técnicas de conteo de pre-cálculo Contar el número de maneras de realizar una tarea es bastante simple - hasta que el número de opciones se hace demasiado grande. Aquí hay tres técnicas de conteo utilizados en pre-cálculo:Permutaciones: ¿De cuántas maneras se pueden elegir r…
¿Cómo encontrar coeficientes binomiales Dependiendo del número de veces que se debe multiplicar el mismo binomio - un valor también conocido como exponente - los coeficientes binomiales para que exponente particular, son siempre los mismos. Los coeficientes binomiales se encuentran…
¿Cómo encontrar probabilidades binomiales utilizando una fórmula estadística Después de identificar que una variable aleatoria X tiene una distribución binomial, es probable que desee encontrar probabilidades para X. La buena noticia es que usted no tiene que encontrarlos a partir del rasguño se llega a utilizar fórmulas…
¿Cómo trabajar con probabilidades en la TI-84 Plus Puede utilizar la TI-84 Plus calculadora gráfica para calcular las probabilidades como permutaciones y combinaciones y generar números enteros y decimales aleatorios. ¿Es necesario para calcular el número de maneras que usted puede organizar…
Esquemas básicos del color para la decoración del hogar Una de las piedras angulares de cualquier proyecto de decoración del hogar es la elección de un esquema de color. Existen combinaciones de colores para todos los gustos. Utilice su rueda de colores para encontrar la combinación de colores…
¿Cómo encontrar colores para el esquema de color de su sitio web La regla básica la mayoría de los esquemas de color para los sitios web es que usted tiene que trabajar con un pequeño número limitado de colores. De lo contrario, su sitio será simplemente presentar una cacofonía desordenada de color. (Sí,…