La teoría de cuerdas: tres dimensiones del espacio
Para entender la teoría de cuerdas, es necesario comprender el significado de las dimensiones adicionales requeridos. En primer lugar, mirar el concepto de las dimensiones de una manera muy general, y los enfoques diferentes matemáticos han utilizado para estudiar el espacio de 2 y 3 dimensiones.
El tiempo es la cuarta dimensión. A continuación, puede analizar las formas en que las dimensiones extra pueden manifestarse en la teoría de cuerdas y si las dimensiones extra son realmente necesarias.
Al buscar en nuestro mundo, tiene tres dimensiones - arriba y abajo, izquierda y derecha, adelante y atrás. Si le das una longitud, latitud y altitud, se puede determinar cualquier lugar de la Tierra, por ejemplo.
Ampliando la idea de la geometría cartesiana, usted encontrará que es posible crear una cuadrícula cartesiana en tres dimensiones, así como dos, como se muestra en esta figura. En una cuadrícula de tal, se puede definir un objeto llamado vector, que tiene tanto una dirección y una longitud. En el espacio 3-dimensional, cada vector está definido por tres cantidades.
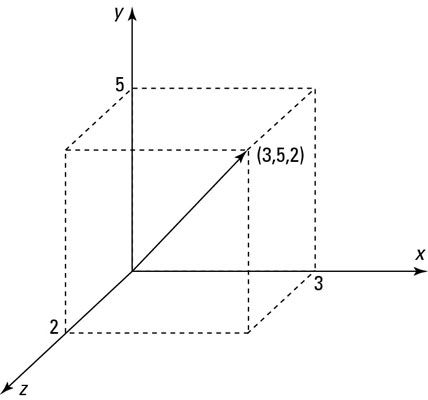
Los vectores pueden, por supuesto, existen en una, dos, o más de tres dimensiones. (Técnicamente, incluso se puede tener un vector de dimensión cero, a pesar de que siempre tendrá una longitud cero y sin dirección. Los matemáticos llaman tal caso " trivial ").
El tratamiento de espacio que contiene una serie de líneas rectas es probablemente una de las operaciones más básicas que pueden tener lugar dentro de un espacio. Un campo de la primera de las matemáticas que se centra en el estudio de los vectores se llama álgebra lineal, que permite analizar los vectores y cosas llamadas espacios vectoriales de cualquier dimensionalidad. (Más matemáticas avanzadas pueden cubrir vectores en más detalle y se extienden en situaciones no lineales.)
Uno de los pasos más importantes de trabajar con los espacios vectoriales es encontrar el base para el espacio vectorial, una manera de definir el número de vectores es necesario definir alguna punto en todo el espacio vectorial. Por ejemplo, un espacio 5-dimensional tiene una base de cinco vectores. Una forma de mirar a la teoría de supercuerdas es darse cuenta de que las direcciones de una cadena puede moverse sólo puede ser descrito con una base de diez vectores distintos, por lo que la teoría describe un espacio vectorial de 10 dimensiones.
-
Cómo mirar la estructura de los vectores en r - Son dimensiones extra realmente necesario para la teoría de cuerdas?
- Bosónico teoría de cuerdas: 25 dimensiones espaciales
- ¿Tiene la teoría de cuerdas describir nuestro universo?
- Más dimensiones hacen el trabajo la teoría de cuerdas
- La teoría de cuerdas: anuncios / correspondencia cft
La teoría de cuerdas: el acceso a otros universos ¿Hay alguna manera de llegar a los cuatro tipos de universos paralelos en la teoría de cuerdas? Siendo realistas, la respuesta es, probablemente, " n, " pero eso no es la opción más interesante. Teóricamente, hay maneras de que algunos de estos…
La teoría de cuerdas y la ley de Einstein de la gravedad Desde la teoría de cuerdas está relacionado con la teoría de la gravedad cuántica, un buen lugar para comenzar es dar una visión general de la comprensión científica de la gravedad, que se define por la teoría de la relatividad general de…
La teoría de cuerdas y branas: estirando una cuerda En cierto sentido, la introducción de la teoría M marca el final de " la teoría de cuerdas, " porque deja de ser una teoría que contiene cadenas solamente fundamentales. M-teoría también contiene membranas multidimensionales, llamados branas.…
La teoría de cuerdas y tres dimensiones del espacio Una forma de mirar a la teoría de supercuerdas es darse cuenta de que las direcciones de una cadena puede moverse sólo puede ser descrito con una base de diez vectores distintos, por lo que la teoría describe un espacio vectorial de 10…
La teoría de cuerdas: el espacio y el tiempo de doblado En la relatividad, la gravedad dobla nuestras cuatro dimensiones del espacio-tiempo, pero en la teoría de cuerdas más dimensiones están obligados en otras formas. El espacio-tiempo es visto como un suave " tela, " pero que el tejido suave se…
La teoría de cuerdas: universos branas Desde el inicio de la teoría de cuerdas, uno de los principales obstáculos conceptuales ha sido la adición de dimensiones extra. Con la introducción de todos estos nuevos objetos, los teóricos de cuerdas han comenzado a explorar lo que…
La teoría de cuerdas define el espacio y el tiempo En muchas versiones de la teoría de cuerdas, las dimensiones extra del espacio se compactificada en un tamaño muy pequeño, por lo que son observables a nuestra tecnología actual. Tratando de mirar en el espacio más pequeño que este tamaño…
La teoría de cuerdas explica la materia y la masa Uno de los principales objetivos de la investigación la teoría de cuerdas actual es construir una solución de la teoría de cuerdas que contiene las partículas que existen realmente en nuestro universo.La teoría de cuerdas que comenzó como una…
La teoría de cuerdas: dentro de un holograma LA holograma es una imagen 2-dimensional que contiene toda la información 3-dimensional de un objeto. Al ver un holograma, puede inclinar la imagen y ver la orientación del movimiento forma. Es como si usted ve el objeto en la imagen desde un…
La teoría de cuerdas hace Dimensiones más tiempo posible Debido a que la relatividad mostró el tiempo como una dimensión del espacio-tiempo y la teoría de cuerdas predice dimensiones espaciales extra, una pregunta natural sería si la teoría de cuerdas predice también (o al menos permite) dimensiones…
La alternativa de la teoría de cuerdas a múltiples dimensiones Hay diferentes maneras en que las dimensiones adicionales requeridos por la teoría de cuerdas puede posiblemente manifiesto y si las dimensiones extra son realmente necesarias. En el enfoque de Gates, que básicamente comercia dimensiones para los…
La teoría de cuerdas: la historia del espacio de 2 dimensiones Uno de los aspectos más fascinantes de la teoría de cuerdas es el requisito de dimensiones extra para hacer el trabajo de la teoría. La teoría de cuerdas requiere nueve dimensiones espaciales, mientras que la teoría M parece requerir diez…