La teoría de cuerdas y tres dimensiones del espacio

Una forma de mirar a la teoría de supercuerdas es darse cuenta de que las direcciones de una cadena puede moverse sólo puede ser descrito con una base de diez vectores distintos, por lo que la teoría describe un espacio vectorial de 10 dimensiones.

Uno de los pasos más importantes de trabajar con los espacios vectoriales es encontrar el base para el espacio vectorial, una manera de definir el número de vectores es necesario definir alguna punto en todo el espacio vectorial. Por ejemplo, un espacio 5-dimensional tiene una base de cinco vectores.

Al buscar en nuestro mundo, tiene tres dimensiones - arriba y abajo, izquierda y derecha, adelante y atrás. Si le das una longitud, latitud y altitud, se puede determinar cualquier lugar de la Tierra, por ejemplo.

Una línea recta en el espacio: Vectores

Ampliando la idea de la geometría cartesiana, usted encontrará que es posible crear una cuadrícula cartesiana en tres dimensiones, así como dos, como se muestra en esta figura. En una cuadrícula de tal, se puede definir un objeto llamado vector, que tiene tanto una dirección y una longitud. En el espacio 3-dimensional, cada vector está definido por tres cantidades.

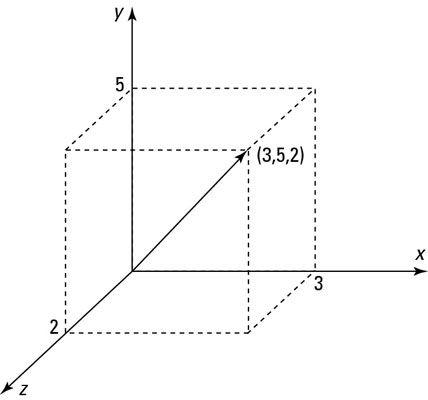
Los vectores pueden, por supuesto, existen en una, dos, o más de tres dimensiones. (Técnicamente, incluso se puede tener un vector de dimensión cero, a pesar de que siempre tendrá una longitud cero y sin dirección. Los matemáticos llaman tal caso " trivial ").

El tratamiento de espacio que contiene una serie de líneas rectas es probablemente una de las operaciones más básicas que pueden tener lugar dentro de un espacio. Un campo de la primera de las matemáticas que se centra en el estudio de los vectores se llama álgebra lineal, que permite analizar los vectores y cosas llamadas espacios vectoriales de cualquier dimensionalidad. (Más matemáticas avanzadas pueden cubrir vectores en más detalle y se extienden en situaciones no lineales.)

Torcer el espacio de 2 dimensiones en tres dimensiones: La cinta de Moebius

En el libro clásico Terreno plano, el personaje principal es un cuadrado (literalmente - que tiene cuatro lados de igual longitud) que gana la habilidad de experimentar tres dimensiones. Tener acceso a las tres dimensiones, puede realizar acciones en una superficie de 2 dimensiones en maneras que parecen muy contradictorio. Una superficie de 2 dimensiones en realidad puede ser torcido de tal manera que no tiene principio ni fin!

El caso más conocido de esto es la Cinta de Moebius, se muestra en esta figura. La cinta de Moebius fue creado en 1858 por los matemáticos alemanes August Möbius y Johann Benedict Listing.

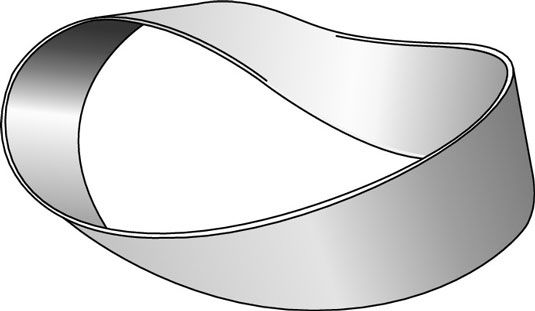
Usted puede crear su propia cinta de Moebius tomando una tira de papel - algo así como una larga marcador - y dándole una media vuelta de tuerca. Luego tomar los dos extremos de la tira de papel y pegarlas juntos. Coloque un lápiz en la mitad de la superficie y dibujar una línea a lo largo de la longitud de la tira sin tomar su lápiz en el papel.

Una cosa curiosa que ocurre a medida que continúe a lo largo. Con el tiempo, sin tomar su lápiz del papel, la línea se dibuja en cada parte de la superficie y, finalmente, se encuentra con sí mismo. No hay " de nuevo " de la cinta de Moebius, que evita de alguna manera la línea de lápiz. Usted ha dibujado una línea a lo largo de toda la forma sin levantar el lápiz.

En términos matemáticos (y las reales, dado el resultado del experimento de lápiz), la tira de Mobius tiene sólo una superficie. No hay " en el interior " y " fuera " de la cinta de Moebius, el camino está en una pulsera. A pesar de que las dos formas pueden parecer iguales, son matemáticamente muy diferentes entidades.

La cinta de Moebius hace, por supuesto, tiene un fin (o cobertura) en cuanto a su anchura. En 1882, el matemático alemán Felix Klein amplió en la idea de cinta de Moebius para crear un Klein botella: una forma que no tiene superficie interior o exterior, pero también tiene límites en cualquier dirección.

Echa un vistazo a esta figura para comprender la botella de Klein. Si usted viajó a lo largo del " frente " de la ruta (con las x), que te finalmente llegar a la " de nuevo " de ese camino (con los o).

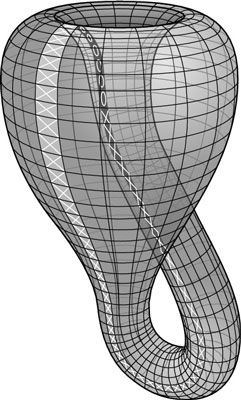
Si usted fuera un salón hormiga en una cinta de Moebius, se podía caminar de su longitud y, finalmente, volver al punto de partida. Caminando su anchura, usted finalmente se encuentra con el " borde del mundo ". Un salón hormiga en una botella de Klein, sin embargo, podría ir en cualquier dirección y, si se acercó lo suficiente, finalmente, encontrarse de vuelta donde empezó. (Viajando por el camino o eventualmente conduce de nuevo a las x.)

La diferencia entre caminar en una botella de Klein y caminar en una esfera es que la hormiga no sería simplemente caminar por el exterior de la botella de Klein, al igual que lo haría en una esfera, pero sería cubrir ambas superficies, al igual que en la cinta de Moebius .