La teoría de cuerdas: la historia del espacio de 2 dimensiones

Uno de los aspectos más fascinantes de la teoría de cuerdas es el requisito de dimensiones extra para hacer el trabajo de la teoría. La teoría de cuerdas requiere nueve dimensiones espaciales, mientras que la teoría M parece requerir diez dimensiones espaciales. Bajo algunas teorías, algunas de estas dimensiones adicionales pueden ser en realidad el tiempo suficiente para interactuar con nuestro propio universo de una manera que pueda ser observado.

Contraste esto con un espacio de 2 dimensiones. Muchas personas piensan de la geometría (el estudio de los objetos en el espacio) como un espacio plano, 2-dimensional que contiene dos grados de libertad - arriba, abajo, derecha o izquierda. A lo largo de la mayor parte de la historia moderna, este interés ha sido el estudio de la geometría euclidiana o geometría cartesiana.

Geometría euclidiana: Piense de nuevo a la geometría de la escuela secundaria

Probablemente el más famoso matemático del mundo antiguo era Euclides, que ha sido llamado el padre de la geometría. Libro 13 volúmenes de Euclides, Elementos, es el primer libro conocido por haber tomado todo el conocimiento existente de la geometría en el momento de su redacción (en torno a 300 aC). Durante casi 2.000 años, la práctica totalidad de la geometría podría entenderse con sólo leer Elementos, que es una de las razones por las que fue el libro de matemáticas de mayor éxito.

En Elementos, Euclides se ubicó en la presentación de los principios de la geometría plana - es decir, la geometría de formas sobre una superficie plana, como en esta figura. Una consecuencia importante de la geometría plana euclidiana es que si se toma la medida de los tres ángulos en el interior de un triángulo, que suman 180 grados.

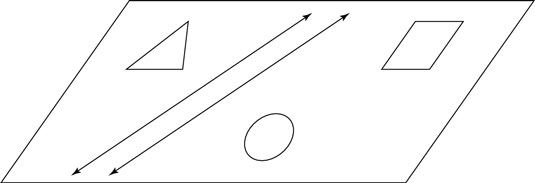
Más adelante en los volúmenes, Euclides se extendió a la geometría 3-dimensional de objetos sólidos, tales como cubos, cilindros y conos. La geometría de Euclides es la geometría normalmente se enseña en la escuela para el día de hoy.

Geometría cartesiana: La fusión de álgebra y geometría euclidiana

La geometría analítica moderna fue fundada por el matemático y filósofo francés René Descartes, cuando puso cifras algebraicas en una cuadrícula física. Esta especie de cuadrícula cartesiana se muestra en esta figura. Mediante la aplicación de los conceptos de la geometría euclidiana a las ecuaciones que aparecen en las rejillas, una visión de la geometría y el álgebra se pudieron obtener.

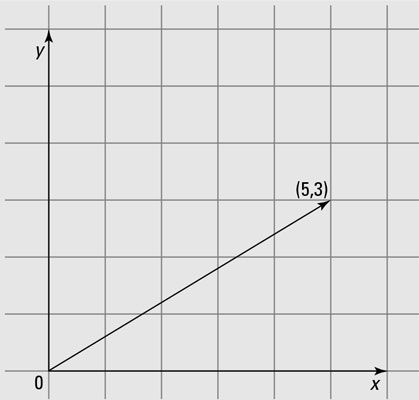
Casi al mismo tiempo que Galileo estaba revolucionando los cielos, Descartes estaba revolucionando las matemáticas. Hasta su trabajo, los campos de álgebra y geometría estaban separados. Su idea era mostrar gráficamente ecuaciones algebraicas, proporcionando una manera de traducir entre la geometría y el álgebra.

Uso de la cuadrícula cartesiana, puede definir una línea por un equation- la línea es el conjunto de soluciones de la ecuación. En la figura, la línea va desde el origen hasta el punto (5, 3). Tanto el origen (0, 0) y (5, 3) son las soluciones correctas a la ecuación representada por la línea (junto con todos los demás puntos de la línea).

Debido a que la rejilla es 2-dimensional, el espacio que la cuadrícula representa contiene dos grados de libertad. En álgebra, los grados de libertad son representados por las variables, lo que significa que una ecuación que se pueden mostrar en una superficie de 2 dimensiones tiene dos cantidades variables, a menudo X y y.