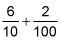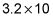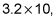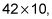Valor decimal maestría en matemáticas núcleo común
En Common Core matemáticas de quinto grado, los estudiantes se basan en lo que han aprendido antes sobre todo # 8208-número de valor posicional, ya que comienzan a estudiar valor decimal - es decir, se estudian los dígitos a la derecha del punto decimal.
Una de las cosas más difíciles acerca de estudiar el valor decimal es que varias de las formas de pensar acerca de los números enteros que los niños comúnmente adoptan no se aplican a los números a la derecha del punto decimal. He aquí dos ejemplos en los decimales se comportan de manera diferente de las expectativas que muchos estudiantes han basado en sus experiencias con números enteros. (Estos ejemplos ilustran por qué no es importante centrarse en reglas, y por qué es importante en vez de centrarse en el significado.)
Para los números enteros, el número con más dígitos es mayor. Con decimales, el número con más dígitos puede ser menor. Cuando se comparan los dos números enteros - por ejemplo, 235 y 62 - el que tiene más dígitos es mayor. Eso es debido a que el 2 en 235 se encuentra en el lugar de las centenas, mientras que 62 no tiene cientos en absoluto. Pero con decimales, la historia es diferente. 0.235 no es mayor que 0,62. Cada vez que se agrega un dígito a la derecha de un número, que agrega un menor el valor de posición - esto es lo contrario del proceso cuando se agrega dígitos a la izquierda del punto decimal.
Los estudiantes tienen que trabajar de manera que mantienen su enfoque en el significado de los lugares con los que trabajan, no sólo en la generación de nuevas reglas para este nuevo entorno. Si los estudiantes forman malos hábitos con decimales, estos hábitos resultan extraordinariamente robustos y difíciles de superar. Es probable que vea a su niño de quinto grado de descomposición decimales (por ejemplo, la escritura 0,62 como
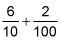
y hacer dibujos con el fin de centrarse en los significados de los números con los que trabajan más que en la memorización de un nuevo conjunto de reglas.
Con el fin de multiplicar por 10, puede agregar un cero en el extremo de todo el número. Al multiplicar decimales por 10, los dígitos se desplazan de un lugar a la izquierda. Al multiplicar 42 por 10, se obtiene 420 - los mismos dígitos, pero con un 0 en el extremo. Este hecho hace que la multiplicación por 10 mucho más fácil que la multiplicación por (por ejemplo) 9. Es una regla importante que hace que los algoritmos de multiplicación posible. Pero no es cierto para los números a la derecha del punto decimal.
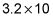
no es igual a 3,20.
Multiplicar decimales por 10 mueve los dígitos un lugar a la izquierda porque ahora representan una cantidad 10 veces mayor que antes. En
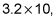
los 3 movimientos de los colocan al lugar de las decenas y los 2 se mueve desde el lugar de los décimos al lugar de las unidades a ser 32. Esto es en realidad lo mismo que sucede cuando se multiplica números enteros también. Cuando multiplicas
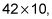
los 4 se mueve desde las decenas colocan al lugar cientos y los 2 se mueve desde los colocan en el lugar decenas de ser 420. Pero entonces el lugar de las unidades está vacío, por lo que llenar ese lugar con un 0. Como siempre en el Núcleo Básico Normas, la atención se centra en el significado de los números, no en el aprendizaje y la aplicación de reglas sin sentido.
Sobre el autor
 Cómo convertir los porcentajes a decimales
Cómo convertir los porcentajes a decimales Porcentajes y decimales son formas muy similares, por lo que todo lo que sabes sobre los decimales lleva más cuando se trabaja con el por ciento. Todo lo que necesitas hacer es convertir su porcentaje a un decimal, y ya está bueno para ir.Para…
 Cómo identificar el valor posicional de los decimales
Cómo identificar el valor posicional de los decimales Con decimales, esta idea detrás del valor posicional de números enteros se extiende. En primer lugar, el punto decimal se coloca a la derecha del lugar de las unidades en un número entero. Entonces más números se añaden a la derecha del punto…
 Cómo multiplicar decimales
Cómo multiplicar decimales Multiplicar decimales es diferente de la suma y resta en que usted no tiene que preocuparse de alinear los puntos decimales. De hecho, la única diferencia entre la multiplicación de números enteros y decimales viene al final.Aquí es cómo…
 Cómo redondear decimales
Cómo redondear decimales Redondeando decimales funciona casi exactamente el mismo que el número de redondeo. Por lo general, necesita para redondear un número decimal o bien a un número entero o para una o dos cifras decimales.Para redondear un número decimal a un…
 Cómo utilizar ceros y ceros a la izquierda en un número decimal
Cómo utilizar ceros y ceros a la izquierda en un número decimal Cuando se trabaja con números decimales, es necesario comprender la diferencia entre ceros y ceros a la izquierda, así como la forma en que afectan el valor del número.Usted probablemente sabe que puede adjuntar ceros al comienzo de un número…
 Mueva el punto decimal para cambiar el valor de un número
Mueva el punto decimal para cambiar el valor de un número Cuando se trabaja con números enteros, se puede multiplicar o dividir cualquier número por 10 con sólo mover el punto decimal a la derecha oa la izquierda, respectivamente. Cuando multiplicas desplazando el punto decimal hacia la derecha,…
 Habilidades decimales básicos necesarios para pasar las pruebas de aritmética
Habilidades decimales básicos necesarios para pasar las pruebas de aritmética Usted necesita saber cómo trabajar con decimales de pasar la mayor parte de las pruebas de aritmética. Cuando usted está agregando o quitando decimales, la forma en que la disposición de su trabajo se vuelve aún más importante de lo normal. Si…
 Matryoshka matemática: contar números, números enteros, números racionales y números reales
Matryoshka matemática: contar números, números enteros, números racionales y números reales Cuando empiece a tratar con números, usted aprenderá acerca de los cuatro grupos principales, o grupos, de números, que, como las muñecas rusas del matryoshka, anidan dentro de otros:Contar números (también llamados números naturales): El…
 Multiplicando con notación científica
Multiplicando con notación científica Multiplicar números que están en notación científica es bastante simple, ya multiplicar potencias de 10 es tan fácil. Aquí es cómo multiplicar dos números que están en notación científica:1. Multiplicar las dos partes decimales de los…
 Preparación ASVAB: cómo multiplicar y dividir decimales
Preparación ASVAB: cómo multiplicar y dividir decimales El ASVAB contiene dos subpruebas de matemáticas. Usted inevitablemente se encontrará con decimales, así que asegúrese de que está preparado y saber cómo multiplicar y dividir decimales y, así como realizar otras operaciones cuando sea…
 Preparación ASVAB: trabajar con decimales
Preparación ASVAB: trabajar con decimales Usted tendrá que saber cómo trabajar con decimales para el asbab. Los decimales son un método de escribir números fraccionarios sin utilizar un numerador y el denominador. Usted puede escribir la fracción 10/07 como el decimal 0,7- lo pronuncia…
 Vuelo Militar prueba de aptitud: decimales
Vuelo Militar prueba de aptitud: decimales Algunas preguntas sobre la prueba de vuelo de Aptitud Militar le requerirán trabajar con decimales. Usted puede expresar una fracción como un porcentaje o decimal. Para convertir una fracción en un decimal, simplemente dividir el numerador entre…