Encuentra un importe de partida de una cantidad final

Algunos problemas de matemáticas le dan la cantidad que usted termina con y le pedirá que averiguar la cantidad que empezó. Estos problemas pueden ser difícil si no estás acostumbrado a pensar hacia atrás. He aquí un ejemplo, y es una especie de una pregunta difícil, por lo que fije el cinturón de seguridad:

María recibió algo de dinero de cumpleaños de su tía. Ella puso el 40% en el banco, pasó del 75% del resto en una bolsa, y cuando terminó, ella tenía $ 12 para gastar en la cena. ¿Cuánto su tía le dio?

En este problema, es necesario empezar por el final y trabajar hacia atrás. Tenga en cuenta que la única cantidad de dólares en el problema viene después de las dos cantidades por ciento. El problema le dice que ella termina con $ 12 después de dos transacciones - que pone el dinero en el banco y la compra de un bolso - y le pide que averigüe lo mucho que comenzó con.

Para resolver este problema, configure dos ecuaciones de palabras para describir las dos transacciones:

El dinero de la tía - el dinero para el banco = dinero después de banco

El dinero luego que el banco - dinero para el bolso = $ 12

Observe lo que estas dos ecuaciones de palabras están diciendo. El primero le dice que María tomó el dinero de su tía, resta algo de dinero para poner en el banco, y se fue al banco con una nueva cantidad de dinero, que se llama dinero después de banco. La segunda ecuación palabra comienza donde el primer deja fuera. Te dice que María tomó el dinero sobrante de la orilla, resta algo de dinero para un bolso, y terminó con $ 12.

Esta segunda ecuación ya tiene una cantidad de dinero rellenado, así que empieza aquí. Para resolver este problema, se da cuenta de que María pasó del 75% de su dinero en ese momento en la bolsa - es decir, el 75% del dinero que aún tenía después que el banco:

El dinero luego que el banco - el 75% del dinero luego que el banco = $ 12

En este ejemplo se va a hacer un pequeño cambio a esta ecuación para que pueda ver lo que está diciendo en realidad:

100% del dinero después de que el banco - el 75% del dinero después de que el banco = $ 12

Adición 100% de no cambia la ecuación, ya que en realidad sólo significa que está multiplicando por 1. De hecho, se puede deslizar estas dos palabras en cualquier lugar sin necesidad de cambiar lo que quieres decir, aunque puede sonar ridículo decir "Ayer por la noche, conduje 100% de mi coche a casa del trabajo, caminó 100% de mi perro, luego tomó el 100% de mi esposa para ver el 100% de una película ".

En este caso particular, sin embargo, estas palabras le ayudan a realizar una conexión ya que el 100% - 75% = 25%. Aquí hay una mejor manera de escribir esta ecuación:

25% del dinero luego que el banco = $ 12

Este le dice que $ 12 dividido por 0,25 le da la cantidad restante de $ 48.

Bueno, usted sabe cuánto dinero Maria tenía después de hacer el depósito bancario, para que pueda conectar este número en la primera ecuación:

El dinero de la tía - el dinero para el banco = $ 48

Ahora usted puede utilizar el mismo tipo de pensamiento para resolver esta ecuación (y va mucho más rápido esta vez!). En primer lugar, María colocó el 40% del dinero de su tía en el banco:

El dinero de la tía - 40% del dinero de la tía = $ 48

Una vez más, vuelve a escribir esta ecuación para hacer lo que dice más claro:

100% del dinero de la tía - 40% del dinero de la tía = $ 48

Ahora, ya que el 100% - 40% = 60%, vuelve a escribir de nuevo:

60% del dinero de la tía = $ 48

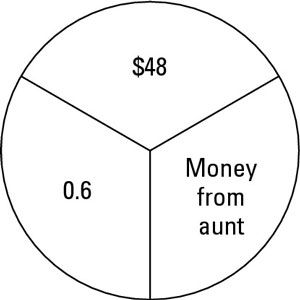
En este punto, se puede utilizar el porcentaje círculo de arriba para resolver la ecuación. En este caso, el porcentaje círculo le dice que $ 48 dividido por 0.6 te da la cantidad restante de $ 80. Así que la tía de María le dio $ 80 para su cumpleaños.