La teoría de cuerdas y variedades de Calabi-Yau

El problema de las dimensiones extra continuó plagando la teoría de cuerdas, pero estos fueron resueltos mediante la introducción de la idea de compactificación, en el que las dimensiones extra enroscan alrededor de la otra, con un crecimiento tan pequeñas que son muy difíciles de detectar.

Las matemáticas sobre cómo esto podría lograrse ya se habían desarrollado en forma de complejo Variedades de Calabi-Yau, un ejemplo del cual se muestra en esta figura. El problema es que la teoría de cuerdas no ofrece ninguna manera verdadera de determinar exactamente cuál de las muchas variedades de Calabi-Yau es correcto!

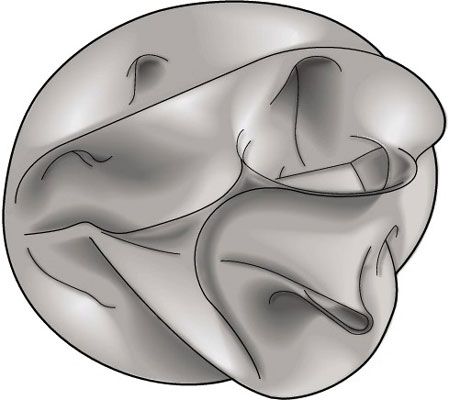
Cuando las dimensiones adicionales fueron descubiertos por primera vez en la década de 1970, estaba claro que deben estar escondidos en alguna manera. Después de todo, ciertamente no vemos más de tres dimensiones espaciales.

Una de ellas fue la que había sido propuesto por Kaluza y Klein medio siglo antes: Las dimensiones podrían ser acurrucados en un tamaño muy pequeño.

Los primeros intentos para acurrucarse estas dimensiones extra toparon con problemas, ya que tienden a mantener la simetría entre la izquierda; y derecho; partículas transmitidas (llamados paridad por físicos), que no siempre se conserva en la naturaleza. Esta violación es crucial para entender la operación de la fuerza nuclear débil.

Para la teoría de cuerdas para trabajar, tenía que haber una manera de compactar las seis dimensiones adicionales al tiempo que conserva una distinción entre la izquierda; partículas mano; zurdos y derechos.

En 1985, las variedades de Calabi-Yau (creadas para otros fines años anteriores por los matemáticos Eugenio Calabi y Shing-Tung Yau) fueron utilizados por Edward Witten, Philip Candelas, Gary Horowitz, y Andrew Strominger para compactar las seis dimensiones espaciales extra por sólo el manera correcta. Estos colectores no sólo conservan el uso de las manos de las partículas, pero también conservan la supersimetría lo suficiente para replicar ciertos aspectos del Modelo Estándar.

Uno de los beneficios de los colectores Calabi-Yau era que la geometría de las dimensiones plegadas da lugar a diferentes tipos de partículas observables en nuestro universo. Si la forma de Calabi-Yau tiene tres agujeros (o más bien análogos de dimensiones superiores de agujeros), tres familias de partículas serán predicha por el modelo estándar de la física de partículas.

Obviamente, por extensión, una forma con cinco agujeros tendrá cinco familias, pero los físicos solamente se ocupa de las tres familias de partículas que saben que existe en este universo.

Por desgracia, hay decenas de miles de posibles variedades de Calabi-Yau de seis dimensiones, y la teoría de cuerdas ofrece ningún medio razonable de determinar cuál es el más adecuado. Por lo demás, aunque los físicos pudieron determinar cuál era el correcto, estarían todavía quiere responder a la pregunta de por qué el universo dobló el extra de seis dimensiones en esa configuración particular.

Cuando variedades de Calabi-Yau se descubrió por primera vez, se esperaba por parte de algunos miembros vocales de la comunidad de la teoría de cuerdas que un colector específico caería como la correcta. Esto no ha demostrado ser el caso, y esto es lo que muchos teóricos de cuerdas habrían esperado en el primer lugar - que el colector específico de Calabi-Yau es una cantidad que tiene que ser determinada por el experimento.

De hecho, ahora se sabe que algunas otras geometrías para espacios dobladas también pueden mantener las propiedades necesarias.