¿Cómo afecta la fricción equilibrio rotatorio

Puede usar la física para calcular la fricción afecta el equilibrio rotacional. Por ejemplo, digamos dueño de una tienda de hardware viene a ti en busca de ayuda con un problema. Un empleado ha subido cerca de la parte superior de una escalera para colgar un cartel de próxima venta de la compañía. El propietario no quiere que la escalera se deslice - pleitos, explica - por lo que le pregunta si la escalera se va a caer.

La situación aparece en la figura. Aquí está la pregunta: ¿La fuerza de fricción mantener la escalera se mueva si theta es de 45 grados y el coeficiente estático de fricción con el suelo es de 0,7?

Hay que trabajar con las fuerzas netas para determinar el par total. Escriba lo que sabe (se puede suponer que el peso de la escalera se concentra en su centro y que se puede descuidar la fuerza de fricción de la escalera contra la pared porque la pared es muy suave):

• F_W = Fuerza ejercida por la pared de la escalera

• F_C = Peso del secretario = 450 N

• F_L = Peso de la escala = 200 N

• F_F = Fuerza de fricción que sostiene la escalera en su lugar

• F_N = Fuerza normal

Es necesario determinar la fuerza necesaria de fricción aquí, y desea que la escalera sea tanto en el equilibrio lineal y rotacional. Equilibrio lineal le indica que la fuerza ejercida por la pared de la escalera, F_W, debe ser la misma que la fuerza de fricción en magnitud pero de sentido opuesto, porque esas son las dos únicas fuerzas horizontales. Por lo tanto, si usted puede encontrar F_W, usted sabe lo que la fuerza de fricción, F_F, necesita ser.

Usted sabe que la escalera está en equilibrio rotacional, lo que significa que

(torque donde neta está representado por la letra griega tau.) Encontrar F_W, echar un vistazo a los pares de todo el fondo de la escala, el uso de ese punto como el punto de pivote. Todos los pares de todo el punto de giro tienen que sumar a cero. La dirección de todos los vectores de par es en el plano perpendicular al plano de la figura, por lo que considera sólo el componente de estos vectores en esa dirección (un componente positivo correspondería a una fuerza de rotación en sentido antihorario en la figura, y un componente negativo sería corresponden a una fuerza de rotación en sentido horario). Debido a que usted está tratando con los componentes del vector, que son números, no se escribe en negrita.

Aquí es cómo encontrar los tres pares de todo el fondo de la escala:

• * Torque debido a la fuerza de la pared contra la escalera. Aquí, r = 4,0 m es la longitud total de la escalera:

  

  Tenga en cuenta que el par de torsión debido a la fuerza de la pared es negativo ya que tiende a producir un movimiento hacia la derecha.

• Par debido al peso del secretario. En este caso, r es de 3,0 metros, la distancia desde la parte inferior de la escalera a la ubicación del empleado:

  

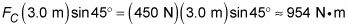
• Torque debido al peso de la escalera. Se puede suponer que el peso de la escalera se concentra en el centro de la escalera, por lo r = 2,0 metros, la mitad de la longitud total de la escalera. Por lo tanto, el par debido al peso de la escalera es

  

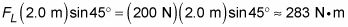
  Estos dos últimos pares son positivos porque las fuerzas generan una fuerza de giro hacia la izquierda, como muestra la figura.

Ahora, debido a

se obtiene el siguiente resultado cuando se suman todos los pares de juntas:

La fuerza de la pared ejerce sobre la escalera es de 437 newtons, que es también igual a la fuerza de fricción de la parte inferior de la escalera en el suelo, porque F_{W # 8232-}y la fuerza de fricción son los únicos dos fuerzas horizontales en todo el sistema. Por Consiguiente,

F_F = 437 N

Usted sabe la fuerza de fricción que usted necesita. Pero, ¿cuánto fricción es lo que realmente tiene? La ecuación básica para la fricción le dice que

dónde

es el coeficiente de fricción estática y F_N es la fuerza normal de la planta que empuja hacia arriba en la escalera, la cual debe equilibrar todas las fuerzas apuntan hacia abajo en este problema porque de equilibrio lineal. Esta # 8232-significa que

F_N = W_C + W_L = 450 N + 200 N = 650 N

El tapar esto en la ecuación para F_{F real} y utilizando el valor de

usted obtiene lo siguiente:

Usted necesita 437 newtons de fuerza, y en realidad se tienen 455 newtons. Buenas noticias - la escalera no se va a caer.