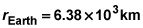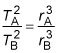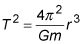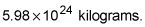Distancia orbital en problemas de física
En física, se puede utilizar la distancia orbital para determinar cuánto tiempo le toma a un objeto para girar en torno a otro. Por ejemplo, se puede calcular el tiempo que tarda Marte para viajar alrededor del Sol, dada su distancia del Sol, en unidades astronómicas.
He aquí algunas preguntas de práctica que puede probar.
Preguntas de práctica
Tierra se encuentra a 1 a.u. (unidad astronómica - una medida de la distancia) de su sol. En las unidades de "años de la Tierra," ¿Cuánto tiempo tarda Marte por su propia revolución solar si se encuentra a 1,5 au ¿Desde el sol?
Redondea tu respuesta a la décima más cercana.
Si la Estación Espacial Internacional se encuentra a 420 kilómetros sobre la superficie de la Tierra, ¿cuántas horas se tarda en hacer una órbita completa?
Utilice los siguientes datos y redondear su respuesta a la centésima más próxima de una hora:
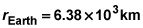
Respuestas
Las siguientes son las respuestas a las preguntas de la práctica:
1.8
La tercera ley de Kepler establece que, habida cuenta de dos cuerpos que orbitan alrededor de A y B, sus periodos (T) de la revolución y distancias (r) del objeto que está girando alrededor están relacionados por la ecuación:
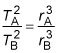
Mientras el partido de unidades en una relación, usted no tiene que convertirlos a "corregir" las unidades de física, por lo que no es necesario convertir los valores unitarios astronómicos a los valores kilómetro. Dado que el período de revolución de la Tierra es de 1 año de la Tierra, la ecuación se resuelve fácilmente por la revolución de Marte en las mismas unidades, que es lo que desea:

1.55 h
Utilice la ecuación que relaciona período orbital a la posición orbital,
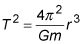
dónde T es el período orbital, r es la distancia entre los centros de la nave y la orbitado, y m es la masa del cuerpo en órbita - en este caso, la Tierra, que tiene una masa de
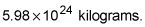
Añadir los 420 kilómetros de radio de la Tierra para calcular la distancia total entre los centros de la Estación Espacial Internacional y de la Tierra, y luego convertir a metros:

Ahora que sustituir en la ecuación orbital, y te encuentras con el período orbital de la Estación Espacial Internacional (en unidades de segundo):

Por último, convertir a hora:
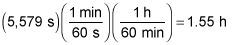
Sobre el autor
 Velocidad angular constante en problemas de física
Velocidad angular constante en problemas de física El uso de la física, puede resolver problemas de velocidad angular constante. Por ejemplo, se puede calcular la rapidez con que un niño se está moviendo en una merry-go-round dado el largo tiempo que toma para que ella viaje alrededor de un lado…
 Fuerza contra la dirección del movimiento en problemas de física
Fuerza contra la dirección del movimiento en problemas de física El uso de la física, se puede calcular la cantidad de trabajo que se hace cuando se aplica una fuerza en la dirección opuesta del movimiento de un objeto. Por ejemplo, si usted se está moviendo una caja, se puede calcular la cantidad de la…
 Fuerza gravitacional en problemas de física
Fuerza gravitacional en problemas de física El uso de la física, se puede calcular la fuerza gravitatoria que se ejerce sobre un objeto por otro objeto. Por ejemplo, dado el peso de, y la distancia entre dos objetos, se puede calcular qué tan grande la fuerza de gravedad se encuentra entre…
 Cómo calcular la velocidad de un satélite alrededor de la tierra
Cómo calcular la velocidad de un satélite alrededor de la tierra En el espacio, la gravedad proporciona la fuerza centrípeta que hace que los satélites (como la luna) en orbitar cuerpos más grandes (como la Tierra). Gracias a la física, si conoce la masa y la altitud de un satélite en órbita alrededor de la…
 Cómo calcular la aceleración centrípeta de un objeto en órbita
Cómo calcular la aceleración centrípeta de un objeto en órbita En física, se puede aplicar primera y segunda ley de Newton para calcular la aceleración centrípeta de un objeto en órbita. Primera ley de Newton dice que cuando no hay fuerzas netas, un objeto en movimiento continuará moviéndose uniformemente…
 Cómo calcular la fuerza de la gravedad en la superficie de la tierra
Cómo calcular la fuerza de la gravedad en la superficie de la tierra A partir de la ecuación de la física de la fuerza de gravedad, se puede conectar en la masa y el radio de la Tierra para calcular la fuerza de gravedad cerca de la superficie de la Tierra.La ecuación de la fuerza de la gravedad esy es verdad, no…
 Cómo calcular el período y el radio orbital de un satélite geosincrónica
Cómo calcular el período y el radio orbital de un satélite geosincrónica Cuando un satélite viaja en una órbita geosíncrona alrededor de la Tierra, que necesita para viajar en un cierto radio orbital y el período para mantener esta órbita. Debido a que el radio y el periodo están relacionados, puede usar la física…
 La energía cinética de los objetos en movimiento en problemas de física
La energía cinética de los objetos en movimiento en problemas de física En física, se puede relacionar la masa, la velocidad de un objeto, y la energía cinética. Por ejemplo, si dos pájaros de diferentes masas están volando a la misma velocidad, se puede calcular cuánto más energía cinética utiliza el más…
 Mediciones y la física
Mediciones y la física Una gran parte de la física tiene que ver con hacer las mediciones - esa es la manera toda la física se inicia. Por esa razón, la física utiliza un número de sistemas de medición, tales como el CGS (centímetro-gramo-segundo) sistema y el MKS…
 Ley de gravitación universal de Newton
Ley de gravitación universal de Newton Sir Isaac Newton se le ocurrió una de las leyes de peso pesado de la física para usted: la ley de la gravitación universal. Esta ley dice que cada masa ejerce una fuerza de atracción sobre todos los otros medios. Si las dos masas son m1 y m2 y…
 La velocidad orbital de problemas de física
La velocidad orbital de problemas de física El uso de la física, se puede calcular la velocidad orbital y el radio de un objeto que gira alrededor de otro. Por ejemplo, dada la velocidad orbital de un satélite alrededor de la Tierra, se puede calcular el radio orbital del satélite.He aquí…
 Período y frecuencia
Período y frecuencia Al describir la manera las cosas van en círculos, no sólo tiene que utilizar radians- también puede especificar el tiempo que tarda. El tiempo que tarda un objeto para completar una órbita se refiere como el período de su movimiento. Período…